
19.(本小题满分14分)
某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5-8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减。
(Ⅰ)下列几个模拟函数中(x表示人均GDP,单位:千美元,y表示年人均A饮料的销量,单位;升),用哪个来描述人均A饮料销量与地区的人均GDP的关系更合适?说明理由。
①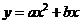 , ②
, ②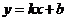 , ③
, ③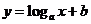 , ④
, ④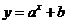
(Ⅱ)若人均GDP为1千美元时,年人均A饮料的销量为2升;若人均GDP为4千美元时,年人均A饮料的销量为5升,把(Ⅰ)中你所选的模拟函数求出来,并求在各个地区中,年人均A饮料的销量最多是多少?
(Ⅲ)因为A饮料在B国被检测出杀虫剂的含量超标,受此事件的影响,A饮料在人均GDP低于3千美元和高于6千美元的地区销量下降5%,其它地区的销量下降10%,根据(Ⅱ)所求出的模拟函数,求在各个地区中,年人均A饮料的销量最多为多少?
18.(本小题满分13分)
设等比数列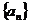 的首项
的首项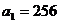 ,前n项和为
,前n项和为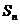 ,且
,且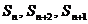 成等差数列.
成等差数列.
(Ⅰ)求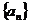 的公比
的公比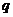 ;
;
(Ⅱ)用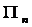 表示
表示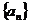 的前
的前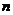 项之积,即
项之积,即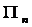
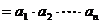 ,试比较
,试比较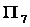 、
、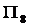 、
、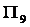 的大小.
的大小.
17. (本小题满分13分)
(本小题满分13分)
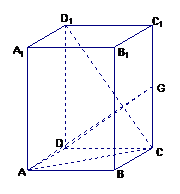
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,
G是CC1上的动点。
(Ⅰ)求证:平面ADG⊥平面CDD1C1
(Ⅱ)判断B1C1与平面ADG的位置关系,并给出证明;
(Ⅲ)若G是CC1的中点,求二面角G-AD-C的大小。
16.(本小题满分12分)
在△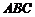 中,已知a、b、
中,已知a、b、 分别是三内角
分别是三内角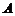 、
、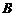 、
、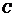 所对应的边长,且
所对应的边长,且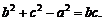
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若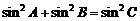 ,试判断△ABC的形状并求角
,试判断△ABC的形状并求角 的大小.
的大小.
15.(几何证明选讲选做题)如图,已知⊙O的割线PAB交⊙O于A,B两
点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为_______________.
14、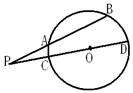 (坐标系与参数方程选做题)曲线
(坐标系与参数方程选做题)曲线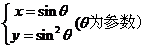 与直线
与直线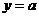 有两个公共点,则实数
有两个公共点,则实数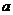 的取值范围是_________________.
的取值范围是_________________.
13、底面边长为2的正三棱锥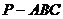 中,E、F、G、H分别是PA、AC、BC、PB中点,则四边形EFGH的面积取值范围是_________。
中,E、F、G、H分别是PA、AC、BC、PB中点,则四边形EFGH的面积取值范围是_________。
12、已知f (x)是定义在实数集R上的函数,且满足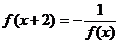 ,
,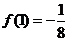 ,
,
则f (2007)=_____ _____.
11、由1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为偶数的共有 个.
10、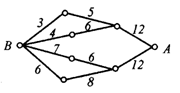 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传送信息,信息可以分开沿不同的路线同时传送,则单位时间内
如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相联,连线标的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传送信息,信息可以分开沿不同的路线同时传送,则单位时间内
传递的最大信息量为( )
A.26 B.24 C.20 D.19
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com