
20.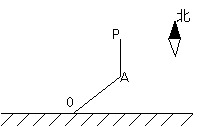 (本小题满分14分)在东西方向直线延伸的湖岸上有一港口O,一艘机艇以40km/h的速度从O港出发,先沿东偏北的某个方向直线前进到达A处,然后改向正北方向航行,总共航行30分钟因机器出现故障而停在湖里的P处,由于营救人员不知该机艇的最初航向及何时改变的航向,故无法确定机艇停泊的准确位置,试划定一个最佳的弓形营救区域(用图形表示),并说明你的理由.
(本小题满分14分)在东西方向直线延伸的湖岸上有一港口O,一艘机艇以40km/h的速度从O港出发,先沿东偏北的某个方向直线前进到达A处,然后改向正北方向航行,总共航行30分钟因机器出现故障而停在湖里的P处,由于营救人员不知该机艇的最初航向及何时改变的航向,故无法确定机艇停泊的准确位置,试划定一个最佳的弓形营救区域(用图形表示),并说明你的理由.
19.(本小题满分14分)已知在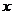 轴上有一点列:
轴上有一点列: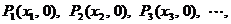
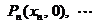 ,点
,点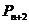 分有向线段
分有向线段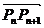 所成的比为
所成的比为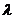 ,其中
,其中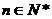 ,
,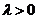 为
为
常数,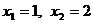 .
.
(1)设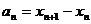 ,求数列
,求数列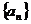 的通项公式;
的通项公式;
(2)设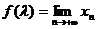 ,当
,当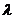 变化时,求
变化时,求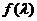 的取值范围.
的取值范围.
18.(本小题满分14分)在四棱锥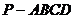 中,
中,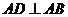 ,
,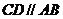 ,
,
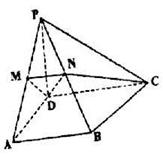
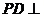 底面
底面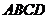 ,
, 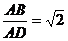 ,直线
,直线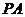 与底面
与底面
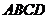 成
成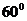 角,点
角,点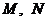 分别是
分别是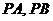 的中点.
的中点.
(1)求二面角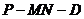 的大小;
的大小;
(2)当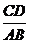 的值为多少时,
的值为多少时,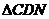 为直角三角形.
为直角三角形.
17.(本小题满分12分)已知函数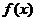 是定义在
是定义在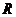 上的偶函数,当
上的偶函数,当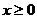 时,
时,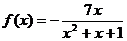 .
.
(1)求当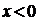 时
时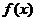 的解析式;
的解析式;
(2)试确定函数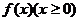 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;
(3)若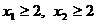 且
且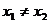 ,证明:
,证明: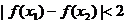 .
.
16.(本题满分12分)将A、B两枚骰子各抛掷一次,观察向上的点数,问:
(I)共有多少种不同的结果?
(II)两枚骰子点数之和是3的倍数的结果有多少种?
(III)两枚骰子点数之和是3的倍数的概率是多少?
15.(几何证明选讲选做题) 15、如图,⊙O的直径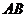 =6cm,
=6cm,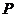 是
是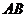 延
延
长线上的一点,过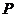 点作⊙O的切线,切点为
点作⊙O的切线,切点为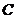 ,连接
,连接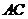 ,
,
若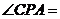 30°,PC =
。
30°,PC =
。
14、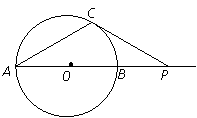 (坐标系与参数方程选做题) 直线
(坐标系与参数方程选做题) 直线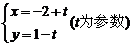 被圆
被圆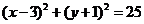 所截得的弦长为
.
所截得的弦长为
.
13. 如图,在正方体ABCD-A1B1C1D1中,点M
如图,在正方体ABCD-A1B1C1D1中,点M
是BC的中点,则D1B与AM所成角的余弦值
是 .
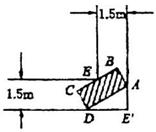
12.如图,一条直角走廊宽为1.5m,一转动灵活的平板手推车,其平
板面为矩形,宽为1m.问:要想顺利通过直角走廊,平板手推车的长
度不能超过 米.
11. 设向量
设向量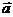 与
与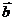 的夹角为
的夹角为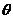 ,
,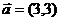 ,
,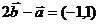 ,
,
则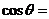 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com