
8、不等式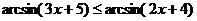 的解集是____________________________。
的解集是____________________________。
7、已知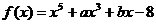 ,且
,且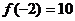 ,则
,则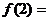 ______________。
______________。
6、已知函数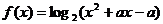 的值域为
的值域为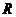 ,则实数
,则实数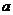 的取值范围是_____________。
的取值范围是_____________。
5、已知函数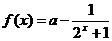 为奇函数,则
为奇函数,则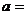 _____________。
_____________。
4、函数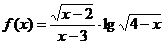 的定义域是_____________________。
的定义域是_____________________。
3、设函数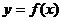 的反函数为
的反函数为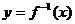 ,若
,若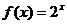 ,则
,则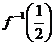 =________。
=________。
2、若1弧度的圆心角所对的弦长等于2,则该圆半径为_______________。
1、集合A=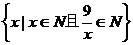 ,则A的非空子集有________个。
,则A的非空子集有________个。
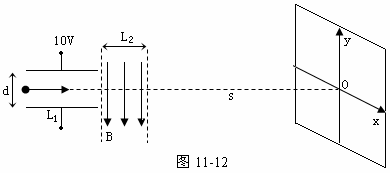
16.如图11-12所示,由电容器和磁场组成一射线管,电容器极板长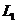 =5cm,两板间距d=5cm,两端加电压U=10V,电容器右侧有一宽度为
=5cm,两板间距d=5cm,两端加电压U=10V,电容器右侧有一宽度为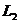 =5cm弱磁场区域,其磁感应强度B=
=5cm弱磁场区域,其磁感应强度B=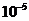 T,方向竖直向下,在磁场边界的右边s=10m处,放置一个标有坐标的屏,现有初速度
T,方向竖直向下,在磁场边界的右边s=10m处,放置一个标有坐标的屏,现有初速度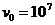 m/s的负离子束从电容器中心水平向右入射(荷质比g =
m/s的负离子束从电容器中心水平向右入射(荷质比g =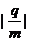 =5×
=5×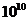 C/kg).若不加电压和磁场时,离子束恰打在坐标的原点上,那么加上电压和磁场后离子束应打在坐标纸上的哪个位置?(结果精确到0.1cm)
C/kg).若不加电压和磁场时,离子束恰打在坐标的原点上,那么加上电压和磁场后离子束应打在坐标纸上的哪个位置?(结果精确到0.1cm)

[解析]通过电场时,粒子受电场力: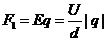
产生加速度: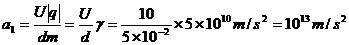 ,方向竖直向上.
,方向竖直向上.
穿出电场的时间: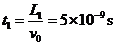 .
.
竖直方向分速度: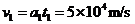 ,又由于L1=5cm
,又由于L1=5cm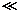 S=10m,故粒子在电容器内沿y轴方向发生的位移可忽略不计,但速度方向发生了偏转,所以在屏上竖直方向的分位移主要是在场外发生.
S=10m,故粒子在电容器内沿y轴方向发生的位移可忽略不计,但速度方向发生了偏转,所以在屏上竖直方向的分位移主要是在场外发生.
 在磁场中,粒子受洛伦兹力:
在磁场中,粒子受洛伦兹力: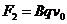 ,其中竖直分速度
,其中竖直分速度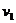 与磁场平行,不会使粒子受洛伦兹力作用.
与磁场平行,不会使粒子受洛伦兹力作用.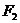 使粒子在水平面内作匀速圆周运动且半径
使粒子在水平面内作匀速圆周运动且半径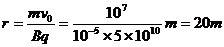 >>
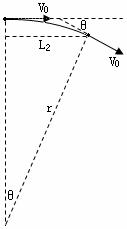
>>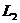 ,所以粒子在磁场中圆周运动的圆心角θ很小,向x轴正方向偏转的位移很小可以忽略,如图所示.同样由于水平方向速度发生偏转,在场外沿x轴正方向的分位移就是屏上的x坐标.
,所以粒子在磁场中圆周运动的圆心角θ很小,向x轴正方向偏转的位移很小可以忽略,如图所示.同样由于水平方向速度发生偏转,在场外沿x轴正方向的分位移就是屏上的x坐标.
在场外沿轴线方向匀速直线运动的时间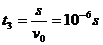 ;
;
纵坐标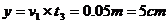 ;
;
在磁场中偏转的速度偏转角等于圆心角,由于θ很小,所以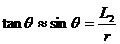 .
.
横坐标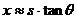
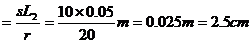 .
.
[答案]2.5cm ,5.0cm
2. 在第二个t0时间内,由于U=0,粒子做匀速圆周运动,根据Bqv=m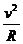
其周期T为:T=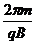 =1×10-4 s,恰好等于t0,在一个周期内恰好回到圆周运动的起点.
=1×10-4 s,恰好等于t0,在一个周期内恰好回到圆周运动的起点.
其轨道半径R=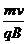 = 0.01 m=1.0 cm,直径是2.0cm,小于射入方向到A板的距离,所以粒子不会碰到A板.
= 0.01 m=1.0 cm,直径是2.0cm,小于射入方向到A板的距离,所以粒子不会碰到A板.
 由此可以判断粒子在第一个t0内作匀速直线运动,在第二个t0内作匀速圆周运动,如此往复,经过5个t0,粒子向前18 cm,还有s/= 0.5 cm才能射出两板,如图所示:
由此可以判断粒子在第一个t0内作匀速直线运动,在第二个t0内作匀速圆周运动,如此往复,经过5个t0,粒子向前18 cm,还有s/= 0.5 cm才能射出两板,如图所示:
粒子经过5t0后做匀速圆周运动的圆心角为θ,则
sinθ=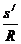 =
=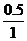 =
=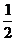 ,所以θ=30°,总时间t=5 t0+
,所以θ=30°,总时间t=5 t0+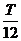 =5.08×10-4 s .
=5.08×10-4 s .
[答案]匀速直线运动,6 cm;5.08×10-4 s.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com