
4.下列句子的排列正确的一项是( )
①例如热河普陀拉的一个窗子,就与无数文艺复兴时代窗子的“ 内容”完全相同,但是各用不同的“词汇”和“文法”,用自己的形式把这样一句“话”说出来了。
②在这里,我打算提出一个各民族的建筑之间的“可译性”的问题。
③又如天坛皇穹宇与罗马的布拉曼提所设计的圆亭子,虽然大小不同,基本上是同一体裁的“文章”。又如罗马的凯旋门与北京的琉璃牌楼,巴黎的一些纪念柱与我们的华表,都是同一性质,同样处理的市容点缀。
④如同语言和文学一样,为了同样的需要,为了解决同样的问题,乃至为了表达同样的情感,不同的民族,在不同的时代是可以各自用自己的“ 词汇”和“ 文法”来处理它们的。
⑤这许多例子说明各民族各有自己不同的建筑手法,建筑出来各种各类的建筑物,如同不同的民族使用不同的文字所写出来的文学作品和通俗文章一样。
⑥简单的如台基、栏杆、台阶等等,所要解决的问题基本上是相同的,但许多民族创造了许多形式不同的台基、栏杆和台阶。
A.⑥③④①②⑤ B.②④⑥①③⑤
C.③④①②⑤⑥ D.②①③⑤⑥④
3.下列各句,没有语病的一项是( )
A.如同语言和文学一样,为了同样的需要,为了表达同样的情感,乃至为了解决同样的问题,不同的民族,在不同的时代是可以各自用自己的“ 词汇”和“ 文法”来处理它们的。
B.虽然我们无论如何也是所有群居性动物中最具社会性的---比蜜蜂更互相依赖,联系更密切,行为上更不可分,我们却并不经常感到我们的联合智慧。
C.本品主要有效成分为茶多酚具有提高细胞抗氧化能力及抗凝血功能的一种自由基清除剂。
D.这个结论即使很有依据,但是如果不能说明地球上的无数生物怎样经历变异而达到它们的相当完善的构造、相互适应,因而难以令人满意。
2.下列各句中加粗的熟语使用恰当的一句是( )
A.中国的建筑体系是在世界各民族数千年文化史中一个无与伦比的建筑体系。
B.南昌一生产酱油的厂家在酱油中添加了人工色素和黏稠剂,却大做广告“ 保证不添加人工色素”,这简直是掩耳盗铃。
C.对应和序列,这两大原理已经深深渗透进全部数学---不只是数学,实际是精密思想的全部领域---之中,交错地编织在我们数系的锦衣玉食之上。
D.这些地区的建筑和中国中心地区的建筑,或是同属于一个体系,或是大同小异,如弟兄之同属于一家的关系。
1.下列各组词语中加粗的字读音完全相同的一组是()
A.劲敌 靓妆 痉挛 不胫而走 曲径通幽
B.和面 迷惑 霍乱 豁然开朗 祸起萧墙
C.峭拔 讥诮 撬动 翘首以待 七窍生烟
D.孝悌 涕泣 剔除 醍醐灌顶 风流倜傥
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
复 习 引 入 |
1、角的概念[0º,360º] 2、从实例出发,发现很多问题中角的范围发生了变化。 |
1、初中是如何定义角的? 从一个点出发引出的两条射线构成的几何图形  这种概念的优点是形象、直观、容易理解,但它是从图形形状来定义角,因此角的范围是 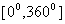 ,这种定义称为静态定义,其弊端在于“狭隘” ,这种定义称为静态定义,其弊端在于“狭隘”2、生活中很多实例会不在该范围 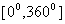 体操运动员转体720º,跳水运动员向内、向外转体1080º 经过1小时时针、分针、秒针转了多少度? 这些例子不仅不在范围 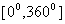 ,而且方向不同,有必要将角的概念推广到任意角,想想用什么办法才能推广到任意角?(运动) ,而且方向不同,有必要将角的概念推广到任意角,想想用什么办法才能推广到任意角?(运动) |
1、引导学生通过切身感受来认识角的概念推广的必要性。 2、为引入正角与负角的概念做好准备。 |
|
新 概 念 产 生 |
1.角的概念的推广 ⑴“旋转”形成角 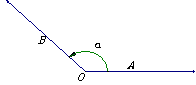 一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到另一位置OB,就形成角α.旋转开始时的射线OA叫做角α的始边,旋转终止的射线OB叫做角α的终边,射线的端点O叫做角α的顶点. 突出“旋转” 注意:“顶点”“始边”“终边” ⑵.“正角”与“负角”“0角” 我们把按逆时针方向旋转所形成的角叫做正角,把按顺时针方向旋转所形成的角叫做负角,如图,以OA为始边的角α=210º,β=-150º,γ=660º, 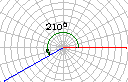 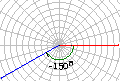 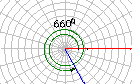 特别地,当一条射线没有作任何旋转时,我们也认为这时形成了一个角,并把这个角叫做零角.记法:角  或 或 可以简记成 可以简记成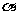  ⑶意义 用“旋转”定义角之后,角的范围大大地扩大了  1° 角有正负之分 如:a=210° b=-150° g=660° 2° 角可以任意大 实例:体操动作:旋转2周(360°×2=720°) 3周(360°×3=1080°) 3° 还有零角 一条射线,没有旋转 角的概念推广以后,它包括任意大小的正角、负角和零角.要注意,正角和负角是表示具有相反意义的旋转量,它的正负规定纯系习惯,就好象与正数、负数的规定一样,零角无正负,就好象数零无正负一样. |
1、教师用多媒体演示角的形成。 2、教师指导学生依定义分别作出大小和方向不同的角,并指出角的“顶点”“始边”“终边” 3、教师设计以下问题组织学生讨论思考回答: (1)正角与负角有何本质区别? (2)正角与负角的实际意义有何不同? (3)角的概念推广以后应该包括哪些角? 4、教师应注意指明:正角与负角是具有相反意义的旋转量,它的正负规定纯系习惯,就好像与正数、负数的规定一样,零角无正负。 |
1、使学生通过亲手作图获取对新概念的直观印象。 2、促使学生从本质上认识角的形成以及角的分类。 3、通过观察旋转绝对量的变化学习角的加减运算。 4、让学生清楚角的正负规定纯系习惯。 |
|
新 概 念 形 成 |
2.“象限角” 为了研究方便,我们往往在平面直角坐标系中来讨论角 角的顶点合于坐标原点,角的始边合于 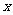 轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限) 轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限)例如:30°、390°、-330°是第Ⅰ象限角,300°、-60°是第Ⅳ象限角,585°、1180°是第Ⅲ象限角,-2000°是第Ⅱ象限角等  |
提出问题,学生讨论回答: (1)在坐标系中表示角时,对角的顶点与角的始边有什么要求? (2)你对“角的终边落在坐标轴上,则此角不属于任何一个象限”这句话是怎么理解的? (3)分别举出几个第一、二、三、四象限角的例子。 |
学习新概念与问题讨论相结合,进一步加深学生对于新概念的理解与掌握。 |
|
新 概 念 形 成 |
3.终边相同的角 ⑴观察:390°,-330°角,它们的终边都与30°角的终边相同 ⑵探究:终边相同的角都可以表示成一个0°到360°的角与 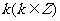 个周角的和: 个周角的和:390°=30°+360° 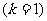 -330°=30°-360° 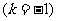 30°=30°+0×360° 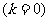 1470°=30°+4×360° 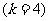 -1770°=30°-5×360° 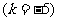 ⑶结论:所有与a终边相同的角连同a在内可以构成一个集合: 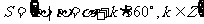 即:任何一个与角a终边相同的角,都可以表示成角a与整数个周角的和 即:任何一个与角a终边相同的角,都可以表示成角a与整数个周角的和 ⑷注意以下四点: (1) 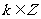 (2) a是任意角; (3) 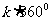 与a之间是“+”号, 与a之间是“+”号,如 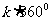 -30º,应看成 -30º,应看成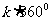 +(-30º); +(-30º);(4)终边相同的角不一定相等,但相等的角,终边一定相同,终边相同的角有无数多个,它们相差360º的整数倍 |
引导学生观察分析: (1)终边相同的角有何特点?(相差整数个周角)。 (2)试表示出与30°终边相同的角。 (3)用集合表示终边相同的角请注意以下问题: ① 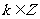 ; ;②a是任意角; ③终边相同的角不一定相等,但是相等的一定终边相同,终边相同的角有无数多个,它们相差360°的整数倍。 |
从观察分析入手,通过具体例子,归纳总结出终边相同的角的表示方法,并初步认识用集合表示终边相同的角需注意的几个问题。 |
|
讲 解 范 例 |
例1 在0º到360º范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角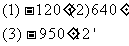  解:⑴∵-120º=-360º+240º, ∴240º的角与-140º的角终边相同,它是第三象限角. ⑵∵640º=360º+280º, ∴280º的角与640º的角终边相同,它是第四象限角. ⑶∵-950º12’=-3 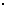 360º+129º48’, 360º+129º48’,∴129º48’的角与-950º12’的角终边相同,它是第三象限角. 例2写出与下列各角终边相同的角的集合S,并把S中在  间的角写出来: 间的角写出来: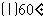 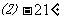 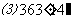  解:(1)  S中在-360º-720间的角是 -1×360º+60º=-280º; 0×360º+60º=60º; 1×360º+60º=420º. (2)  S中在-360º-720间的角是 0×360º-21º=-21º; 1×360º-21º=339º; 2×360º-21º=699º. (3)  S中在-360º-720º间的角是 -2×360º+363º14’=-356º46’; -1×360º+363º14’=3º14’; 0×360º+363º14’=363º14’. |
1、选例1的第一小题板书来示范解题的步骤,其他例题请几个学生板演,,其他学生在下面自己完成,针对板演同学所出现的步骤上的问题及时给予更正,教师要适时引导学生做好总结归纳。 2、例2可以组织学生讨论,然后让学生回答,互相更正,对出现的错误进行纠正讲解,并要求学生熟练掌握这些常见角的集合的表示方法。 |
1、例1主要让学生学会如何在0º到360º范围内,找出与某个角终边相同的角,并判断它是哪个象限的角。 2、例4主要想解决:所有与a终边相同的角连同a在内可以构成一个集合: 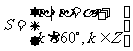 即:任何一个与角a终边相同的角,都可以表示成角a与整数个周角的和。在这里: 即:任何一个与角a终边相同的角,都可以表示成角a与整数个周角的和。在这里:① 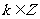 ; ;②a是任意角; ③终边相同的角不一定相等,但是相等的一定终边相同,终边相同的角有无数多个,它们相差360°的整数倍。 |
|
课 堂 练 习 |
1.锐角是第几象限的角?第一象限的角是否都是锐角?小于90º的角是锐角吗?0º-90º的角是锐角吗? (答:锐角是第一象限角;第一象限角不一定是锐角;小于90º的角可能是零角或负角,故它不一定是锐角;0º-90º的角可能是零角,故它也不一定是锐角.) 总结有关角的集合表示. 锐角:{θ|0º<θ<90º}, 0º-90º的角:{θ|0º≤θ≤90º}; 小于90º角:{θ|θ<90º}. 2.已知角的顶点与坐标系原点重合,始边落在x轴的正半轴上,作出下列各角,并指出它们是哪个象限的角? (1)420º,(2)-75º,(3)855º,(4)-510º. (答:(1)第一象限角,(2)第四象限角,(3)第二象限角,(4)第三象限角) 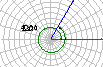 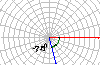 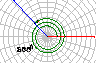 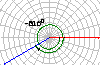 |
|
课堂练习的目的是对本节课的内容进行综合回顾,教师可以放手让学生自行解决,然后教师加以点拨。 |
|
归 纳 小 结 |
从知识、方法两个方面对本节课的内容进行归纳总结。 |
本节课我们学习了正角、负角和零角的概念,象限角的概念,要注意如果角的终边在坐标轴上,就认为这个角不属于任何象限.本节课重点是学习终边相同的角的表示法.严格区分“终边相同”和“角相等”;“轴线角”“象限角”和“区间角”;“小于90º的角”“第一象限角”“0º到90º的角”和“锐角”的不同意义. |
请学生在教师的叙述回顾中再现本节的核心内容。 |
|
课 后 作 业 |
1.下列命题中正确的是( ) A.终边在y轴非负半轴上的角是直角 B.第二象限角一定是钝角 C.第四象限角一定是负角 D.若β=α+k·360º(k∈Z),则α与β终边相同 2.与120º角终边相同的角是( ) A.-600º+k·360º,k∈Z B.-120º+k·360º,k∈Z C.120º+(2k+1)·180º,k∈Z D.660º+k·360º,k∈Z 3.若角α与β终边相同,则一定有( ) A.α+β=180º B.α+β=0º C.α-β=k·360º,k∈Z D.α+β=k·360º,k∈Z 4.与1840º终边相同的最小正角为 ,与-1840º终边相同的最小正角是 . 5.今天是星期一,100天后的那一天是星期 ,100天前的那一天是星期 . 6.钟表经过4小时,时针与分针各转了 (填度). 7.在直角坐标系中,作出下列各角 (1)360º (2)720º (3)1080º (4)1440º 8.已知A={锐角},B={0º到90º的角},C={第一象限角},D={小于90º的角}. 求A∩B,A∪C,C∩D,A∪D. 9.将下列各角表示为α+k·360º(k∈Ζ,0º≤α<360º)的形式,并判断角在第几象限. (1)560º24′ (2)-560º24′ (3)2903º15′ (4)-2903º15′ (5)3900º (6)-3900º |
本次作业主要涉及以下重要内容: 1、正角、负角、象限角的基本概念; 2、终边相同的角的概念及终边相同的角的集合表示法。 这些内容对以后的学习有很重要的作用,请同学们认真落实完成。 |
通过作业让学生巩固以下三点: 1、角的概念推广后的范围; 2、弄清角的分类; 3、终边相同的角的集合表示法。 |
本节主要介绍推广角的概念,引入正角、负角、零角的定义,象限角的概念以及终边相同的角的表示方法.树立运动变化的观点,理解静是相对的,动是绝对的,并由此深刻理解推广后的角的概念.教学方法可以选用讨论法,通过实际问题,教师抽象并通过用几何画板多媒体课件演示角的形成更加形象直观,如螺丝扳手紧固螺丝、时针与分针、车轮的旋转等等,都能形成角的概念,给学生以直观的印象,形成正角、负角、零角的概念,明确“规定”的实际意义,突出角的概念的理解与掌握.通过具体问题,让学生从不同角度作答,理解终边相同的角的概念,并给以表示,从特殊到一般,归纳出终边相同的角的表示方法,达到突破难点之目的.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com