
8.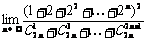 等于:(A)16 (B)8 (C)4 (D)2
等于:(A)16 (B)8 (C)4 (D)2
7.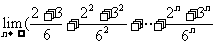 )等于
( )
)等于
( )
(A)0
(B) ¥
(C)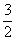 (D)5
(D)5
3.在等比数列{an}中,a1>1,且前n项和Sn满足 ,那么a1的取值范围是( )(98年)
,那么a1的取值范围是( )(98年)
(A)(1,+∞) (B)(1,4) (C)(1,2) (D)(1,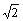 )
)
2.
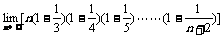 的值等于(
)(91年)
的值等于(
)(91年)
(A)0 (B)1 (C)2 (D)3
例1.用数学归纳法证明2n>n2 (n∈N,n³5),则第一步应验证n= ;
例2.用数学归纳法证明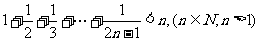 ,第一步验证不等式 成立;
,第一步验证不等式 成立;
例3.是否存在常数a,b,c,使得等式1·22+2·32+……+n(n+1)2=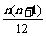 (an2+bn+c)对一切自然数n成立?并证明你的结论.(89年)
(an2+bn+c)对一切自然数n成立?并证明你的结论.(89年)
例4.已知数列{an}=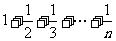 ,记Sn=a1+a2+a3+…+an,用数学归纳法证明Sn=(n+1)an-n.
,记Sn=a1+a2+a3+…+an,用数学归纳法证明Sn=(n+1)an-n.
例5.证明: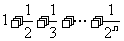 >
>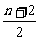 (n∈N,n³2)
(n∈N,n³2)
例6.证明:xn─nan─1x+(n─1)an能被(x─a)2整除(a≠0).
例7.在1与2之间插入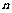 个正数
个正数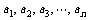 ,使这
,使这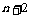 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入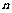 个正数
个正数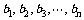 使这
使这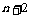 个数成等差数列.记
个数成等差数列.记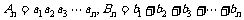 .
.
(Ⅰ)求数列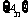 和
和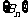 的通项;(Ⅱ)当
的通项;(Ⅱ)当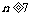 时,比较
时,比较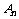 与
与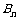 的大小,并证明你的结论.
的大小,并证明你的结论.
例8.若数列{an}满足对任意的n有:Sn=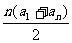 ,试问该数列是怎样的数列?并证明你的结论.
,试问该数列是怎样的数列?并证明你的结论.
例9.已知数列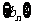 是等差数列,
是等差数列,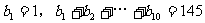 。
。
(Ⅰ)求数列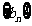 的通项
的通项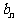 ;(Ⅱ)设数列
;(Ⅱ)设数列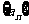 的通项
的通项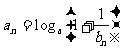 (其中
(其中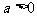 ,且
,且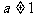 ),记
),记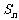 是数列
是数列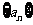 的前n项和。试比较
的前n项和。试比较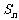 与
与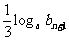 的大小,并证明你的结论。
的大小,并证明你的结论。
练习(数列的极限)
1.
已知{an}是等比数列,如果a1+a2+a3=18,a2+a3+a4=-9,Sn=a1+a2+……+an,那么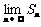 的值等于( )(89年)
的值等于( )(89年)
(A)8 (B)16 (C)32 (D)48
例1.(1)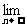
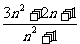 =
;
=
;
(2)数列{an}和{bn}都是公差不为0的等差数列,且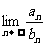 =3,则
=3,则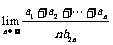 =
=
(3)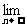
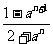 (a>1)=
;
(a>1)=
;
(4)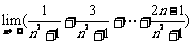 =
;
=
;
(5)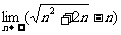 =
;
=
;
(6)等比数列{an}的公比为q=─1/3,则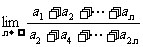 = ;
= ;
例2.将无限循环小数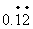 ;1.32
;1.32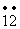
 化为分数.
化为分数.
例3.已知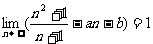 ,求实数a,b的值;
,求实数a,b的值;
例4.数列{an},{bn}满足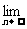 (2an+bn)=1,
(2an+bn)=1, 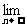 (an─2bn)=1,试判断数列{an},{bn}的极限是否存在,说明理由并求
(an─2bn)=1,试判断数列{an},{bn}的极限是否存在,说明理由并求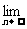 (anbn)的值.
(anbn)的值.
例5.设首项为a,公差为d的等差数列前n项的和为An ,又首项为a,公比为r的等比数列前n项和为Gn ,其中a≠0,|r|<1.令Sn=G1+G2+…+Gn,若有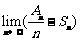 =a,求r的值.
=a,求r的值.
例6.设首项为1,公比为q(q>0)的等比数列的前n项之和为Sn,又设Tn=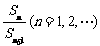 ,求
,求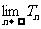 .
.
例7.{an}的相邻两项an,an+1是方程x2─cnx+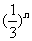 =0的两根,又a1=2,求无穷等比c1,c2,…cn, …的各项和.
=0的两根,又a1=2,求无穷等比c1,c2,…cn, …的各项和.
例8.在半径为R的圆内作内接正方形,在这个正方形内作内切圆,又在圆内作内接正方形,如此无限次地作下去,试分别求所有圆的面积总和与所有正方形的面积总和。
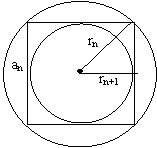
例9.如图,B1,B2,…,Bn,…顺次为曲线y=1/x(x>0)上的点,A1,A2,…,An…顺次为ox轴上的点,且三角形OB1A1,三角形A1B2A2,三角形An─1BnAn为等腰三角形(其中Ð Bn为直角),如果An的坐标为(xn,0).
(1)求出An的横坐标的表达式;
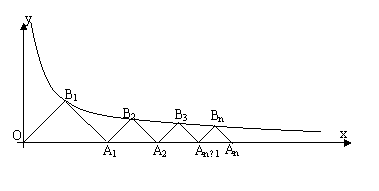 (2)求
(2)求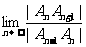 .
.
(二)数学归纳法
数学归纳法是证明与自然数n有关命题的一种常用方法,其证题步骤为:
①验证命题对于第一个自然数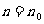 成立。
成立。
②假设命题对n=k(k≥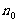 )时成立,证明n=k+1时命题也成立.
)时成立,证明n=k+1时命题也成立.
则由①②,对于一切n≥ 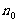 的自然数,命题都成立。
的自然数,命题都成立。
(一) 数列的极限
1.定义:对于无穷数列{an},若存在一个常数A,无论预选指定多么小的正数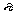 ,都能在数列中找到一项aN,使得当n>N时,|an-A|<
,都能在数列中找到一项aN,使得当n>N时,|an-A|<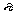 恒成立,则称常数A为数列{an}的极限,记作
恒成立,则称常数A为数列{an}的极限,记作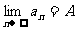 .
.
2.运算法则:若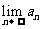 、
、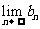 存在,则有
存在,则有
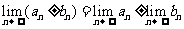 ;
;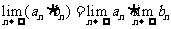
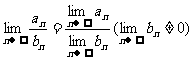
3.两种基本类型的极限:<1> S=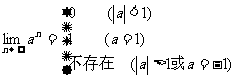
<2>设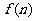 、
、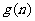 分别是关于n的一元多项式,次数分别是p、q,最高次项系数分别为
分别是关于n的一元多项式,次数分别是p、q,最高次项系数分别为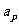 、
、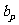 且
且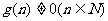 ,则
,则
4.无穷递缩等比数列的所有项和公式: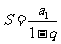 (|q|<1)
(|q|<1)
无穷数列{an}的所有项和: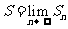 (当
(当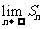 存在时)
存在时)
27.图14为两个半岛示意图,回答下列问题。(10分)


(1)如果某海轮从港口A走最近便的航海线到港口B,应依次经过哪些著名海峡?(4分)
(2)简要分析影响A、B两港口的共同区位因素。(6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com