4．熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质，并能用它研究复合函数的性质．

3．掌握三角变换公式在三角形中应用的特点，并能结合三角形的公式解决一些实际问题．

2．熟悉三角变换常用的方法--化弦法，降幂法，角的变换法等．并能应用这些方法进行三角函数式的求值、化简、证明．

1．熟练掌握三角变换的所有公式，理解每个公式的意义，应用特点，常规使用方法等．

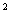角的概念的推广，弧度制； 任意角的三角函数，单位圆中的三角函数线，同角三角函数的基本关系式：sina+cos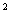a=1， sin a/cos a=tan a，　 tan a cot a=1，正弦、余弦的诱导公式；两角和与差的正弦、余弦、正切，二倍角的正弦、余弦、正切；正弦函数、余弦函数的图象和性质，周期函数，函数y=Asin(ωx+ψ)的图象，正切函数的图象和性质，已知三角函数值求角；正弦定理，余弦定理，斜三角形解法举例。 　二、考试要求 　 　1．理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算。 　　 2　 掌握任意角的正弦、余弦、正切的定义，了解余切、正割、余割的定义，掌握同解三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义。 　　 3．掌握两角和与两角差的正弦、余弦、正切公式，掌握二倍角的正弦、余弦、正切公式。 　　 4．能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明。 　　 5．了解正弦函数、余弦函数、正切函数的图象和性质，会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+ψ)的简图，理解A、ω、ψ的物理意义。 　　 6．会由已知三角函数值求角，并会用符号arcsin x, arcos x,arctan x表示。 　　 7．掌握正弦定理、余弦定理，并能初步运用它们解斜三角形，能利用计算器解决解三角形的计算问题。

23.在“沙砾”、“星星”、“蜡烛”上任选一种，仿照下面《溪流》格式，写一组句子。(2005年江苏卷第22题)(3分)

溪流

没有江河奔腾的浪花，

也没有大海壮阔的波澜，

但山石间的那点叮咚，

是你欢快的旋律。

22.“小灵通”这一通讯工具，与移动电话相比，它具有固定电话的优势---接听电话不收费用；与固定电话相比，它又具有移动电话的许多优点，比如，可随身携带，能收发短信息。写一则广告词，宣传“小灵通”的以上优点。要求：①至少运用一种修辞手法，力求耐人寻味；②16字以内。(2 分)