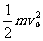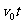9．设弹性势能为E，固定时：E=　 ①，s=②，

不固定时：E=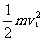+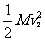③，0=mv₁+Mv₂④， x=(v₁+v₂)t⑤，由①②③④⑤得x=．

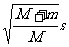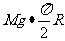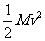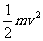8．由机械能守恒定律得：－mgR=+ ①，v=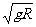 ②，由①②得．

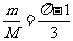7．水平方向的分速度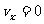 ，竖直方向的分速度．

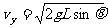2.3动量和能量(一)(答案)

[例题]例1．(1)设PO′=x，当0<x≤Lcosθ时可使小球绕钉来回摆动．

(2) 小球绕钉做圆周运动的半径r=L－x，在圆周运动的最高点速度v≥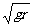①，

由动能定理得：mg[L(1－cosθ)－2 r]= 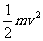－0②，由①②得当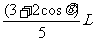≤x≤L时可使小球绕钉做圆周运动．

例2．(1)设b球在最低点时所在的水平面为参考平面，则由机械能守恒定律得：

mg×2L+ mg×2L = mg×L+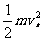+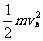①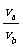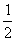，=②，由①②得，．

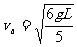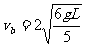(2)a球机械能不守恒。对a球由动能定理得： mgL+W=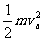－0，得W=－．

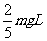例3．动量守恒；Mv₀=(M+m)v　 ①

(1)对小铁块由动能定理得：W₁=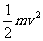－0　 ②，由①②得摩擦力对小铁块做的功W₁=．

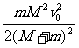(2)木板克服摩擦力做的功W₂=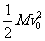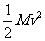－ 　③，由①③得W₂=．

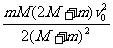(3)系统减少的机械能ΔE=－=．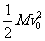

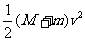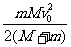(4)系统增加的内能Q=ΔE=．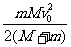

(5)恰好没有滑离长木板，则Q=fs_相对=μmg L=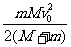，即木板长度L=．

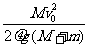变化；系统增加的内能Q=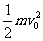，水平力对系统做的功W=．

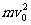[练习]1．D　2．A　3．ABD　4．AD　5．B　6．D　

11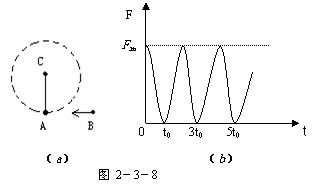．如图2－3－8(a)所示为一根竖直悬挂的不可伸长的轻绳，下端拴一小物块A，上端固定在C点且与一能测量绳的拉力的测力传感器相连．已知一质量为m₀的子弹B沿水平方向以速度v₀射入A内(未穿透)，接着两者一起绕C点在竖直平面内做圆周运动．在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图所示(b)，已知子弹射入的时间极短，且图2中t=0为A、B开始以相同速度运动的时刻，根据力学规律和题中(包括图)提供的信息，对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量，你能求得哪些定量的结果？

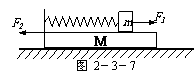
10．如图2－3－7所示，一劲度系数为k的轻弹簧左端固定在长木板M的左端，右端与小物块m连接，且M、m及M与水平地面间接触均光滑．开始时，m和M均静止，现同时对m、M施加等大反向的水平恒力F₁和F₂，F₁=F₂=F．设整个过程中弹簧的形变不超过弹性限度，m未滑离M．求：

(1)当长木板M的位移为L时，M、m及弹簧组成的系统具有的机械能是多少？

(2)如长木板M的位移L是未知的，则当L是多少时，由M、m及弹簧组成的系统具有的机械能最大．这时系统具有的机械能是多少？

9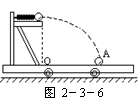．如图2－3－6所示，在水平光滑桌面上放一质量为M的玩具小车。在小车的平台(小车的一部分)上有一质量可忽略的弹簧，一端固定在平台上，另一端用质量为m的小球将弹簧压缩一定距离后用细线捆住．用手将小车固定在桌面上，然后烧断细线，小球就被弹出，落在车上A点．OA＝s．如果小车不固定而烧断细线，球将落在车上何处？设小车足够长，球不致落在车外．

8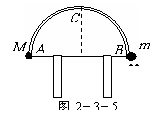．如图2－3－5所示，一轻绳两端各系一小球(可视为质点)，质量分别为M和m(M>m)，跨放在一个光滑的半圆柱上．两球由水平直径AB的两端由静止开始释放，当m到达圆柱体侧面最高点C处时，恰好能脱离圆柱体，试求两球质量之比？

7．如图2－3－4所示，长为L的轻绳，一端用轻环套在水平光滑的横杆上(轻绳与轻环的质量都忽略不计)，另一端连接一质量为m的小球．开始时，将系球的绳子绷紧并转到与横杆平行位置，然后轻轻放手．当绳子与横杆成θ角时小球速度在水平方向和竖直方向的分量大小各是多少？

6．如图2－3－3所示，某海湾共占面积1.0×10⁷m²，涨潮时平均水深20m，此时关上闸门可使水位保持20m不变．退潮时，坝外降至18m．利用此水坝建立一座双向水力发电站，重力势能转化为电能的效率为10%，每天有两次涨潮，该电站每天能发出的电能是(g=10m/s²)　　　　　　　　　　　　　　　　 (　　　 )

A、2.0×10¹⁰J

B、4.0×10¹⁰J

C、8.0×10¹⁰J

D、1.6×10¹¹J