
3. 函数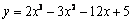 在区间[0,3]上的最大值与最小值为( )
在区间[0,3]上的最大值与最小值为( )
A.5,– 15 B.5,– 4 C.– 4,– 15 D.5,– 16
2. 在等比数列{an}中,已知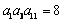 ,则
,则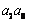 等于( )
等于( )
A.16 B.6 C.12 D.4
1. 已知集合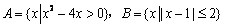 ,那么集合
,那么集合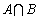 等于( )
等于( )
A.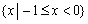 B.
B.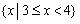
C.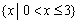 D.
D.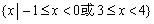
2、 《练习册》 P 33 3
四、 小结
运用二次函数的知识解决实际问题中的最大值。
五、 作业
《练习册》 P 33 2
六、 教学后记
1、 《练习册》 P 32 1
3、 能够对解决问题的基本策略进行反思
教学重点和难点
重点:运用二次函数的知识解决实际问题中的最大值
难点:解决此类问题的基本思路
教学过程设计
一、 从学生原有的认知结构提出问题
一个矩形,当周长一定时,它的面积有时可很大,有时可很小,但什么时候最大呢。这节课,我们就研究这个问题。
|
二、 师生共同研究形成概念
1、 讲解例题
例1 一条长为60cm的铁丝围成一个矩形,求当一条边长为多少时,矩形的面积最大。
分析:此例是为下面的讲解作铺垫。可由学生自己画图,再通过计算求得结果。
2、 书本引例
此处可用设计好的课件演示给学生看,学生容易接受,再探讨课本问题。
☆ 议一议 书本P 62 议一议
结果都是一样的。
3、 做一做
☆ 做一做 书本P 62 做一做
这类问题都比较抽象,建议教学时要向学生说清道理。
☆ 议一议 书本P 63 议一议
解决此类问题的基本思路是
(1) 理解问题;
(2) 分析问题中的变量和常量,以及它们之间的关系;
(3) 用数学的方式表示它们之间的关系;
(4) 做数学求解;
(5) 检验结果的合理性、拓展等
4、 讲解例题
例2 书本 P 63 习题2.8 2
分析:此例较难,要通过相似,得出结果。
三、 随堂练习
2、 能够分析和表达不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题中的最大值
1、 经历探索长方形和窗户透光最大面积问题的过程,进一步获得利润数学方法解决实际问题的经验,并进一步感受数学模型思想和数学的应用价值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com