6. 下列函数关系中，是二次函数的是(　 )

A.在弹性限度内，弹簧的长度y与所挂物体质量x之间的关系

B.当距离一定时，火车行驶的时间t与速度v之间的关系

C.等边三角形的周长C与边长a之间的关系

D.圆心角为120°的扇形面积S与半径R之间的关系

	6.17	6.18	6.19	6.20

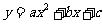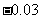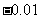5.(08恩施)将一张边长为30㎝的正方形纸片的四角分别剪去一个边长为x㎝的小正方形，然后折叠成一个无盖的长方体.当x取下面哪个数值时，长方体的体积最大

(　　 )　 A.　 7　　　　 B.　 6　　　　　 C.　 5　　　　　 D.　 4

4. 苹果熟了，从树上落下所经过的路程s与下落的时间t满足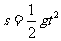(g是不为0的常数)则s与t的函数图象大致是(　　 )

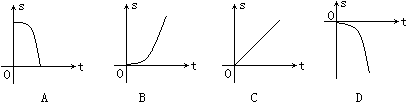
3. 矩形周长为16cm, 它的一边长为xcm，面积为ycm²，则y与x之间函数关系为　　　 ．

2. 某飞机着陆生滑行的路程s米与时间t秒的关系式为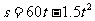：，试问飞机着陆后滑行　　　　　 米才能停止.

1.(06浙江)二次函数y＝x²+10x－5的最小值为　　　　　　 ．

3．二次函数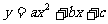通过配方可得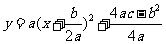，其抛物线关于直线　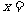　 对称，顶点坐标为(　　　　 ，　 　　　).

⑴ 当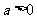时，抛物线开口向　　　 ，有最　　 (填“高”或“低”)点, 当

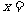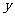　　　 时，有最　　 (“大”或“小”)值是　　　　　 　；

⑵ 当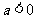时，抛物线开口向　　　 ，有最　　 (填“高”或“低”)点, 当

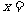　　　　 时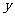，有最　　 (“大”或“小”)值是　　　 　　　．

[典例精析]

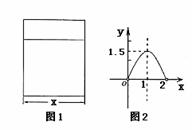例1 用铝合金型材做一个形状如图1所示的矩形窗框，设窗框的一边为x m，窗户的透光面积为y m²，y与x的函数图象如图2所示.

⑴ 观察图象，当x为何值时，窗户透光面积最大？

⑵ 当窗户透光面积最大时，窗框的另一边长是多少？

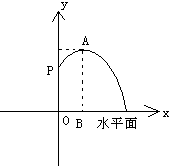例2 橘子洲头要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP＝3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米.

(1)求这条抛物线的解析式；

(2)若不计其它因素，水池的半径至少要多少米，

才能使喷出的水流不至于落在池外？

[中考演练]

2. 顶点式的几种特殊形式.　

⑴ 　　　　　　　　， ⑵ 　　　　　　　　， ⑶ 　　　　　　，(4)　　　　　　 .

1. 二次函数的解析式：(1)一般式：　　　　　　 ；(2)顶点式： 　　　　　　　　；

　　　　　　　　　 (3)交点式：　　　　　　　 .

4. 把一段长1.6米的铁丝围长方形ABCD，设宽为x，面积为y．则当y最大时，x所取的值是(　 　)　

A．0.5　 　　　B．0.4　 　　　　 C．0.3 　　　　 　D．0.6

[考点链接]