
2.对数的概念
思考:1 为什么对数的定义中要求底数 ,且
,且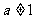 ;
;
2 对数式与指数式的互化:
对数式 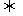 指数式
指数式
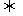
←
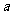 →
→
←
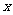 →
→
← 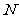 →
→
3 是否是所有的实数都有对数呢?
(四)解答题:
7.求函数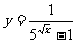 的定义域.
的定义域.
8.(选作)已知函数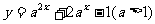 在区间[-1,1]上的最大值是14,求a的值.
在区间[-1,1]上的最大值是14,求a的值.
(三)填空题:
4.函数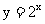 与函数
与函数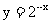 的图像关于
对称.
的图像关于
对称.
5.解不等式: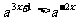
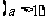 的解集是
。
的解集是
。
6.已知函数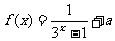 ,
,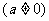 为奇函数,则a=
.
为奇函数,则a=
.
(二)选择题:
1、若指数函数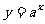 在[-1,1]上的最大值与最小值的差是1,则底数a等 ( )
在[-1,1]上的最大值与最小值的差是1,则底数a等 ( )
A.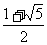 B.
B. 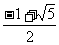 C.
C.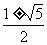 D.
D. 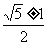
2.函数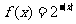 的值域是 ( )
的值域是 ( )
A.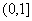 B.
B.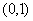 C.
C.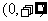 D.R
D.R
3.函数 ,满足
,满足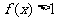 的
的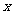 的取值范围 ( )
的取值范围 ( )
A.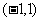 B.
B. 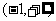 C.
C.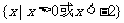 D.
D.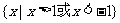
(一)复习:(提问)
1.指数函数的图象及性质
重点:指数函数性质
难点:指数函数性质的运用
⑴ 理解指数函数的概念和意义
⑵能借助计算器或计算机画出具体指数函数的图像
⑶探索并理解指数函数的单调性与特殊点
⑷ 在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型。
8.(选作)已知函数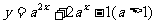 在区间[-1,1]上的最大值是14,求a的值.
在区间[-1,1]上的最大值是14,求a的值.
7.求函数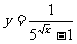 的定义域.
的定义域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com