基础知识归纳：集合的初步知识包括集合的有关概念、简单集合的表示及集合同集合之间的关系．

(1)集合的基本概念

①集合的元素

某些指定的对象集在一起就成为一个集合，集合中的每个对象叫做这个集合的元素．如果a是集合A的元素，就说a属于集合A，记作 a∈A．

不含任何元素的集合叫做空集，记作 ．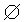

②集合可分为有限集与无限集．

③集合的表示法：列举法、描述法以及图示法．

④常见数集：N(自然数集)、Z(整数集)、Q(有理数集)、R(实数集)．

(2)集合与集合的关系

①对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，就说集合B包含集合A，记作A B，这时也说集合A是集合B的子集．

对于两个集合 A与 B，如果 A B，且 B A，那么A=B．

②补集：如果A S，那么 A在S中的补集

CSA={x|x∈S，且x A}．

全集：如果一个集合含有要研究的各个集合的全部元素，这个集合就可以看作一个全集，全集通常用U表示．

③交集：A∩B={x|x∈A，且x∈B}．并集：A∪B={x|x∈A，或x∈B}．

1．数集A满足条件：若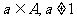，则.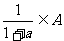

　　　 ①若2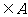，则在A中还有两个元素是什么；

　　　 ②若A为单元集，求出A和.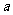

重点：集合的关系

　　 难点： 集合的运算

理解集合的表示法，

会进行集合间的基本运算

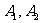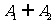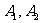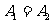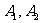5．集合满足=A，则称()为集合A的一种分拆，并规定：当且仅当时，()与(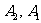)为集合A的同一种分拆，则集合A={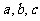}的不同分拆种数为多少？

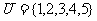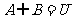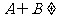
4．已知全集，若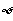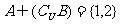，，，试写出满足条件的A、B集合.

3．设集合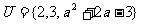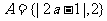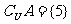，，，求实数a的值.

2．设，，.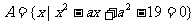

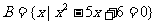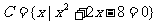　　　 ①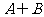=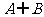，求a的值；

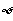
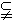
　　　 ②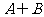，且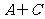=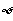，求a的值；

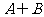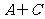
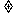
　　　 ③=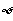，求a的值；

1．数集A满足条件：若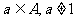，则.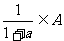

　　　 ①若2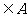，则在A中还有两个元素是什么；

　　　 ②若A为单元集，求出A和.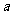

(四)作业 　课本P₄₄习题A组　 6　 B组　 3

(三)小结

本节主要学习了函数的奇偶性，判断函数的奇偶性通常有两种方法，即定义法和图象法，用定义法判断函数的奇偶性时，必须注意首先判断函数的定义域是否关于原点对称，单调性与奇偶性的综合应用是本节的一个难点，需要同学们结合函数的图象充分理解好单调性和奇偶性这两个性质．