(五)归纳小结

1.函数的概念

2.函数的三要素

3.函数的定义域与值域的求解

4.两个函数相等

(二)、新课讲解

函数的定义域通常是由问题的实际背景确定的，如前面所述的三个实例。如果只给出解析式y=f(x),而没有指明它的定义域，那么函数的定义域就是指能使这个式子有意义的实数的集合。

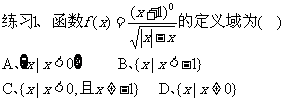
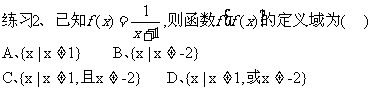
求定义域的几种情况

(1)如果f(x)是整式，那么函数的定义域是实数R　 (2)如果f(x)是分式，那么函数的定义域是使分母不等于0的实数的集合　　　　　　　　　　　　　　　　　　　　　　 (3)如果f(x)是二次根式，那么函数的定义域是使根号内的式子大于或等于0的实数的集合　　　　　　 (4)如果f(x)是由几个部分的数学式子构成的，那么函数的定义域是使各部分式子都有意义的实数集合.(即求各集合的交集)

函数值的集合{f(x)| x∈A }叫做函数的值域

例1、求函数 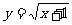的值域

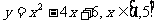例2、求函数 的值域

例3、函数　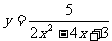 的值域为(　　 D )

A、 (-∞,5］　　　　 B、 (0,+ ∞)

C、［5,+ ∞)　　　　 D、(0,5]

练习、

1、函数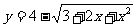 的值域为(　 C　 )

A、(-∞,2］　　　　　　　　 B、(-∞ ,4］　　

C、［2,4］　　　　　　　　 D、［2, +∞)　　

2、求函数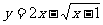的值域

(一)、复习提问：

1、函数的概念　 2、函数的三要素3、如何判断两个函数是否为同一函数

体会对应关系在刻画函数概念中的作用；会求一些简单函数的定义域和值域，并熟练使用区间表示法 .

2、求函数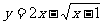的值域

1、函数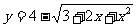 的值域为(　 )

A、(-∞,2］　　　　　　　　 B、(-∞ ,4］　　

C、［2,4］　　　　　　　　 D、［2, +∞)　　

3、如何判断两个函数是否为同一函数

二新课预习

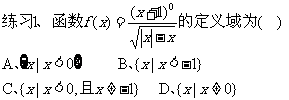
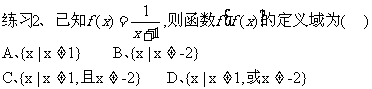
例1、求函数 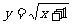的值域

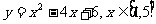例2、求函数 的值域

例3、函数　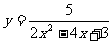 的值域为(　　 )

A、 (-∞,5］　　　　 B、 (0,+ ∞)

C、［5,+ ∞)　　　　 D、(0,5]

练习、

2、函数的三要素

1、函数的概念

(四)作业 　　P₂₇习题1.2(A组)1、2、3、4 (B组)第1题