
2.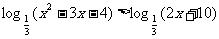
(-2<x<1或4<x<7)
1.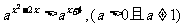
(当a>1时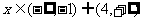 当0<a<1时
当0<a<1时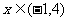 )
)
解:原不等式可化为: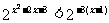 ∵底数2>1
∵底数2>1
∴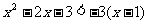 整理得:
整理得: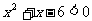
解之,不等式的解集为{x|-3<x<2}
例二 解不等式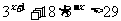
解:原不等式可化为: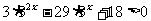
即: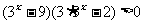 解之:
解之: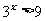 或
或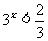
∴x>2或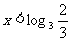 ∴不等式的解集为{x|x>2或
∴不等式的解集为{x|x>2或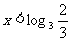 }
}
例三 解不等式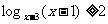
解:原不等式等价于  或
或
解之得:4<x≤5
∴原不等式的解集为{x|4<x≤5}
例四 解关于x的不等式: 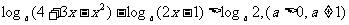
解:原不等式可化为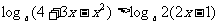
当a>1时有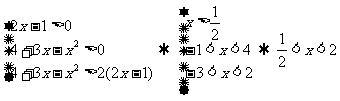
(其实中间一个不等式可省)
当0<a<1时有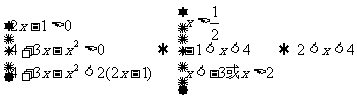
∴当a>1时不等式的解集为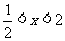 ;
;
当0<a<1时不等式的解集为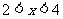
例五 解关于x 的不等式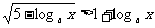
解:原不等式等价于
Ⅰ: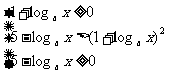 或 Ⅱ:
或 Ⅱ: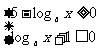
解Ⅰ: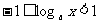 解Ⅱ:
解Ⅱ: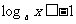 ∴
∴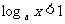
当a>1时有0<x<a 当0<a<1时有x>a
∴原不等式的解集为{x|0<x<a, a>1}或{x|x>a, 0<a<1}
例六 解不等式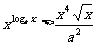
解:两边取以a为底的对数:
当0<a<1时原不等式化为: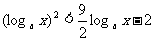
∴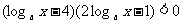
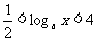 ∴
∴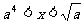
当a>1时原不等式化为: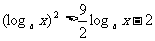
∴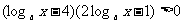
∴ 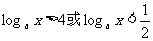 ∴
∴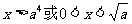
∴原不等式的解集为
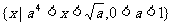 或
或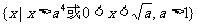
强调:利用指数不等式与对数不等式的单调性解题
因此必须注意它们的“底”及它们的定义域
5、假如你是第二个邮递员,看了这篇文章,会引发哪些思考?
4、作者塑造第一个邮递员运用了哪些描写方法?请任选其一结合相关语句谈谈它的作用。
3、本文写了三个邮递员,为什么却以《两个邮递员》为题?
2、当第二个邮递员让作者为他写一篇报道时,为什么作者觉得有些困难?
15.设实数x、y满足不等式组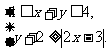
(1)求点(x,y)所在的平面区域;
(2)设 ,在(1)所求的区域内,求函数
,在(1)所求的区域内,求函数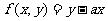 的最值
的最值
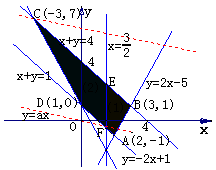 解:(1)已知的不等式组等价于
解:(1)已知的不等式组等价于
解得点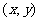 所在的平面区域为所示的阴影部分(含边界)
所在的平面区域为所示的阴影部分(含边界)
其中,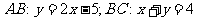

(2)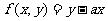 表示直线
表示直线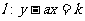 在y轴上的截距,且直线
在y轴上的截距,且直线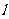 与(1)中所求区域有公共点
与(1)中所求区域有公共点
∵ ,∴当直线
,∴当直线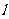 过顶点C时,
过顶点C时,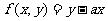 最大
最大
∵C点的坐标为(-3,7),∴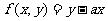 的最大值为
的最大值为
如果-1<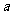 ≤2,那么当直线
≤2,那么当直线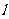 过顶点A(2,-1)时,
过顶点A(2,-1)时,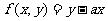 最小,最小值为-1-2
最小,最小值为-1-2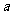 .
.
如果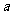 >2,那么当直线
>2,那么当直线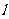 过顶点B(3,1)时,
过顶点B(3,1)时,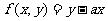 最小,最小值为1-3
最小,最小值为1-3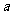
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com