
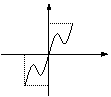
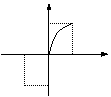
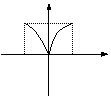
5、(2002上海)函数 的大致图象是----------------------( )
的大致图象是----------------------( )
|
 y
y
y
y
y
y
y
y
 π
π
π
π
π
π
-π
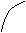 o π x -π
o π
x -π o π x -π o π x
o π x -π
o π
x -π o π x -π o π x
-π -π -π
(A) (B) (C) (D)
4、(2002江苏)在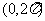 内,使
内,使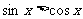 成立的
成立的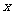 取值范围为-----------------( )
取值范围为-----------------( )
(A) (B)
(B) 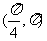 (C)
(C) 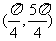 (D)
(D)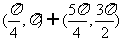
3.(2003北京)已知函数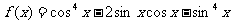
(1) 求f(x)的最小正周期;
(2)
若xÎ[0,  ],求f(x)的最大值,最小值.
],求f(x)的最大值,最小值.
2.(2003北京春季)在DABC中,已知A、B、C成等差数列,求  的值.
的值.
1.(2003
江苏)已知xÎ(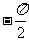 ,0),cosx=
,0),cosx=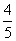 ,则tan2x = ------------------------------(
)
,则tan2x = ------------------------------(
)
A. 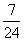 B.
B. 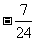 C.
C. 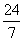 D.
D.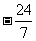
例1、已知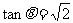 ,求(1)
,求(1)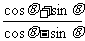 ;(2)
;(2)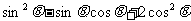 的值.
的值.
解:(1)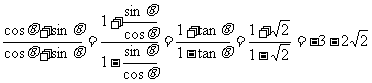 ;
;
(2) 
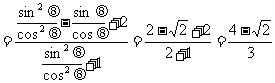 .
.
说明:利用齐次式的结构特点(如果不具备,通过构造的办法得到),进行弦、切互化,就会使解题过程简化。
例2、已知函数f(x)=tan(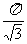 sinx)
sinx)
(1)求f(x)的定义域和值域;
(2)在(-π,π)中,求f(x)的单调区间;
(3)判定方程f(x)=tan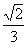 π在区间(-π,π)上解的个数。
π在区间(-π,π)上解的个数。
解:(1)∵-1≤sinx≤1 ∴ - 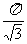 ≤
≤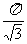 sinx≤
sinx≤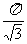 。又函数y=tanx在x=kπ+
。又函数y=tanx在x=kπ+ (k∈Z)处无定义,
(k∈Z)处无定义,
且 (- ,
, )
)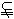 [-
[-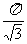 ,
,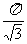 ]
]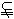 (-π, π),
(-π, π),
∴令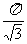 sinx=±
sinx=± ,则sinx=±
,则sinx=±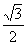
解之得:x=kπ±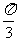 (k∈Z)
(k∈Z)
∴f(x)的定义域是A={x|x∈R,且x≠kπ±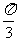 ,k∈Z}
,k∈Z}
∵tanx在(- ,
, )内的值域为(-∞,+∞),而当x∈A时,函数y=
)内的值域为(-∞,+∞),而当x∈A时,函数y=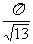 sinx的值域B满足
sinx的值域B满足
(- ,
, )
)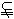 B
B
∴f(x)的值域是(-∞,+∞)。
(2)由f(x)的定义域知,f(x)在[0,π]中的x=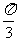 和x=
和x=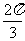 处无定义。
处无定义。
设t=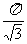 sinx,则当x∈[0,
sinx,则当x∈[0, 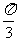 )∪(
)∪(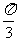 ,
,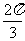 )∪(
)∪(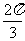 ,π)时,t∈[0,
,π)时,t∈[0, 
 ∪(
∪( ,
,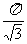
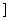 ,且以t为自变量的函数y=tant在区间(0,
,且以t为自变量的函数y=tant在区间(0, ),(
),( ,
,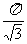
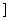 上分别单调递增。
上分别单调递增。
又∵当x∈[0,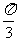 ]时,函数t=
]时,函数t=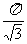 sinx单调递增,且t∈[0,
sinx单调递增,且t∈[0, 

当x∈(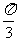 ,
,
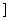 时,函数t=
时,函数t=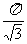 sinx单调递增,且t∈(
sinx单调递增,且t∈( ,
, 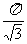
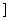
当x∈[ ,
,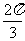
 时,函数t=
时,函数t=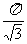 sinx单调递减,且t∈(
sinx单调递减,且t∈( ,
, 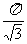
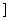
当x∈(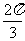 ,π)时,函数t=
,π)时,函数t=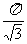 sinx单调递减,且t∈(0,
sinx单调递减,且t∈(0, )
)
∴f(x)=tan(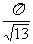 sinx)在区间[0,
sinx)在区间[0,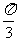
 ,(
,(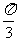 ,
,
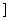 上分别是单调递增函数;在
上分别是单调递增函数;在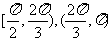 上是单调递减函数。
上是单调递减函数。
又f(x)是奇函数,所以区间(-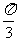 ,0
,0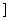 ,[-
,[- ,-
,-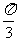
 也是f(x)的单调递增区间
也是f(x)的单调递增区间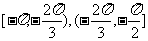 是f(x)的递减区间。
是f(x)的递减区间。
故在区间(-π,π)中,f(x)的单调递增区间为:[- ,-
,-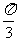
 ,(-
,(-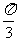 ,
,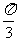 ),(
),(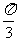 ,
,
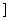 单调递减区间为
单调递减区间为 。
。
(3)由f(x)=tan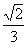 π得:
π得:
tan(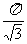 sinx)=tan(
sinx)=tan(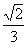 π)
π)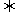
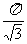 sinx=kπ+
sinx=kπ+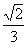 π (k∈Z)
π (k∈Z)
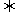 sinx=k
sinx=k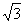 +
+ (k∈Z)①
(k∈Z)①
又∵-1≤sinx≤1,∴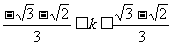
∴k=0或k= -1
当k=0时,从①得方程sinx=
当k=1时,从①得方程sinx= -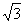 +
+
显然方程sinx= ,sinx=
-
,sinx=
-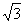 +
+ ,在(-π, π)上各有2个解,故f(x)=tan
,在(-π, π)上各有2个解,故f(x)=tan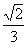 π在区间(-π,π)上共有4个解。
π在区间(-π,π)上共有4个解。
说明:本题是正弦函数与正切函数的复合。(1)求f(x)的定义域和值域,应当先搞清楚y=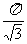 sinx的值域与y=tanx的定义域的交集;(2)求f(x)的单调区间,必须先搞清f(x)的基本性质。如奇偶性、周期性、复合函数单调性等。
sinx的值域与y=tanx的定义域的交集;(2)求f(x)的单调区间,必须先搞清f(x)的基本性质。如奇偶性、周期性、复合函数单调性等。
例3 、已知函数 的定义域为
的定义域为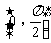 ,值域为 [ -5,1 ],求常数a、b的值.
,值域为 [ -5,1 ],求常数a、b的值.
解:∵ 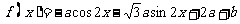 ,
,
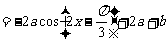 .
.
∵  ,∴
,∴  ,∴
,∴ 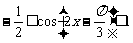 .
.
当a > 0时,b ≤ f ( x ) ≤ 3a + b,
∴ 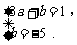 解得
解得 
当a < 0时,3a + b ≤ f ( x ) ≤ b .
∴ 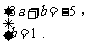 解得
解得 
故a、b的值为 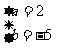 或
或 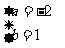
说明:三角函数作为函数,其定义域和值域也是它的要素,要待定表达式中的常数值,需注意常数变化对值域的影响.
例4、设 的周期
的周期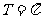 ,最大值
,最大值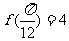 ,
,
(1)求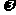 、
、 、
、 的值;
的值;
(2)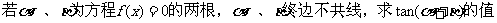 .
.
解:(1) 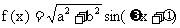 ,
, 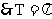 ,
, 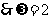 , 又
, 又 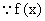 的最大值
的最大值
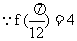 ,
,
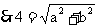 ① ,
且
① ,
且 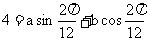 ②,
②,
由 ①、②解出 a=2 , b=3.
(2)
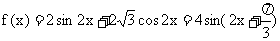 ,
, 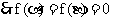 ,
,
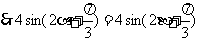 ,
,
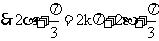 , 或
, 或 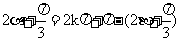 ,
,
即  (
(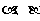 共线,故舍去) , 或
共线,故舍去) , 或 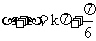 ,
,
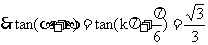
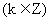 .
.
说明:方程组的思想是解题时常用的基本思想方法;在解题时不要忘记三角函数的周期性。
例5、已知:sin3α+cos3α=1,求sinα+cosα; sin4α+cos4α;sin6α+cos6α的值。
解法一:令sinα+cosα=t,则sinα·cosα=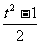
∴sin3α+cos3α=(sinα+cosα)(sin2α-sinα·cosα+cos2α)
=t·(1-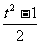 )=1,得:
)=1,得:
t3-3t+2=0 (t-1)2·(t+2)=0
(t-1)2·(t+2)=0
∵t≠-2 ∴t=sinα+cosα=1,且sinα·cosα=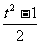 =0。
=0。
∴sin4α+cos4α=(sin2α+cos2α)2 – 2sin2α·cos2α=1-2·0=1
sin6α+cos6α=(sin2α+cos2α)(sin4α-sin2α·cos2α+cos4α)=1
解法二:∵sin3α≤sin2α,cos3α≤cos2α
∴sin3α+cos3α≤sin2α+cos2α=1
等号当且仅当 时成立,
时成立,

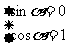 或
或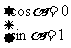
∴sinα+cosα=sin4α+cos4α=sin6α+cos6α=1
说明:(1)凡是遇到sinx+cosx与sinx·cosx类的问题,均应采用换元法,令sinx+cosx=t,得sinx·cosx=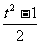 。
。
(2)三角中的恒等变形与初中所学整式的恒等变形结合是解本题的关键所在。
(3)本题还可推广到一般情形:若k≥2且sin2k-1α+cos2k-1α=1,则sinα=1,cosα=0或sinα=0,cosα=1,若sin2kα+cos2kα=1,则sinα=±1,cosα=0或sinα=0,cosα=±1。
例6、设f(x)=tanx,x∈(0,  ),若x1,x2∈(0,
),若x1,x2∈(0, ),且x1≠x2,证明:
),且x1≠x2,证明:
 [ f(x1)+ f(x2)]>f(
[ f(x1)+ f(x2)]>f(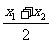 )
)
证明:tanx1+
tanx2= +
+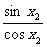 =
=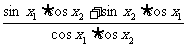
= ∵x1,x2∈(0,
∵x1,x2∈(0, ),且x1≠x2
),且x1≠x2
∴2sin(x1+x2)>0,cosx1·cosx2>0,0<cos(x1-x2)<1
从而有0<cos(x1+x2)+cos(x1-x2)<1+cos(x1+x2)
∴tan x1+tanx2>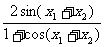 =2tan
=2tan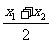
另证:以上是采用化弦,放缩后利用公式tan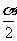 =
=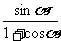 加以证明的,也可以利用正切的和差角公式加以证明。
加以证明的,也可以利用正切的和差角公式加以证明。
左边-右边= [tanx1+tanx2]-tan
[tanx1+tanx2]-tan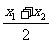
= [tanx1-tan
[tanx1-tan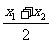 +tanx2-tan
+tanx2-tan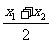 ]
]
= [tan(x1-
[tan(x1-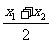 )·(1+tanx1·tan
)·(1+tanx1·tan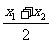 )+tan(x2-
)+tan(x2-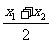 )·(1+tanx2·tan
)·(1+tanx2·tan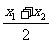 )]
)]
= tan
tan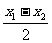 ·(1+tanx1tan
·(1+tanx1tan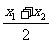 -1-tanx2·tan
-1-tanx2·tan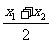 )
)
= tan
tan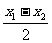 tan
tan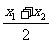 (tanx1-tanx2) ,∵
(tanx1-tanx2) ,∵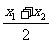 ∈(0,
∈(0,  ) ∴tan
) ∴tan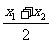 >0
>0
又∵tan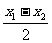 和tanx1-tanx2在x1>x2时,同为正,在x1<x2时,同为负,所以tan
和tanx1-tanx2在x1>x2时,同为正,在x1<x2时,同为负,所以tan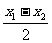 (tanx1-tanx2)>0。
(tanx1-tanx2)>0。
综上 tan
tan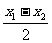 tan
tan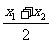 ·(tanx1-tanx2)>0,即
·(tanx1-tanx2)>0,即 [f(x1)+f(x2)]>f(
[f(x1)+f(x2)]>f(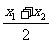 )
)
说明:在三角函数恒等式、条件等式、不等式证明中,常采用化弦法。本题解法一是化弦,了解决把两个分数的单角转化为和角,同时又使函数值适当缩小。
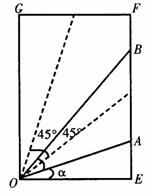 例7、如图,A、B是一矩 OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=
例7、如图,A、B是一矩 OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=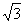 ,设∠AOE=α.
,设∠AOE=α.
(1)写出△AOB的面积关于α的函数关系式f(α);
(2)写出函数f(x)的取值范围。
解:(1)∵OE=1,EF=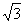
∴∠EOF=60°
当α∈[0,15°]时,△AOB的两顶点A、B在E、F上,且AE=tanα,BE=tan(45°+α)
∴f(α)=S△AOB= [tan(45°+α)-tanα]
[tan(45°+α)-tanα]
= =
=
当a∈(15°,45°]时,A点在EF上,B点在FG上,且OA=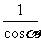 ,OB=
,OB=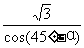
∴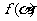 =S△AOB=
=S△AOB= OA·OB·sin45°=
OA·OB·sin45°= ·
·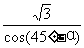 ·sin45°=
·sin45°=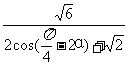
综上得:f(α)= 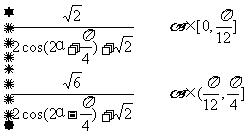
(2)由(1)得:当α∈[0,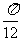 ]时
]时
f(α)= 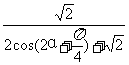 ∈[
∈[ ,
,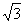 -1]
-1]
且当α=0时,f(α)min= ;α=
;α=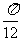 时,f(α)max=
时,f(α)max=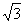 -1;
-1;
当α∈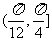 时,-
时,-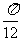 ≤2α-
≤2α-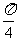 ≤
≤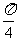 ,f(α)=
,f(α)= ∈[
∈[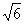 -
-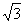 ,
,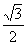 ]
]
且当α=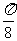 时,f(α) min=
时,f(α) min=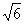 -
-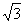 ;当α=
;当α=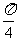 时,f(α) max=
时,f(α) max=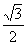
所以f(x) ∈[ ,
,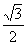 ]。
]。
说明:三角函数与其他数学知识有着紧密的关系,它几乎渗透了数学的每一个分支。练习时注意三角函数的综合应用。
例8、 已知函数y= cos2x+
cos2x+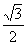 sinx·cosx+1 (x∈R),
sinx·cosx+1 (x∈R),
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图像可由y=sinx(x∈R)的图像经过怎样的平移和伸缩变换得到?
解:(1)y= cos2x+
cos2x+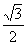 sinx·cosx+1=
sinx·cosx+1= (2cos2x-1)+
(2cos2x-1)+  +
+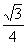 (2sinx·cosx)+1
(2sinx·cosx)+1
= cos2x+
cos2x+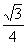 sin2x+
sin2x+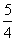 =
= (cos2x·sin
(cos2x·sin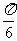 +sin2x·cos
+sin2x·cos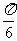 )+
)+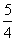
= sin(2x+
sin(2x+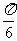 )+
)+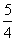
所以y取最大值时,只需2x+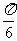 =
= +2kπ,(k∈Z),即 x=
+2kπ,(k∈Z),即 x=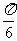 +kπ,(k∈Z)。
+kπ,(k∈Z)。
所以当函数y取最大值时,自变量x的集合为{x|x=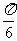 +kπ,k∈Z}
+kπ,k∈Z}
(2)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图像向左平移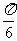 ,得到函数y=sin(x+
,得到函数y=sin(x+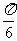 )的图像;
)的图像;
(ii)把得到的图像上各点横坐标缩短到原来的 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+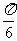 )的图像;
)的图像;
(iii)把得到的图像上各点纵坐标缩短到原来的 倍(横坐标不变),得到函数y=
倍(横坐标不变),得到函数y= sin(2x+
sin(2x+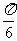 )的图像;
)的图像;
(iv)把得到的图像向上平移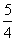 个单位长度,得到函数y=
个单位长度,得到函数y= sin(2x+
sin(2x+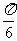 )+
)+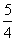 的图像。
的图像。
综上得到y= cos2x+
cos2x+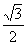 sinxcosx+1的图像。
sinxcosx+1的图像。
说明:本题是2000年全国高考试题,属中档偏容易题,主要考查三角函数的图像和性质。这类题一般有两种解法:一是化成关于sinx,cosx的齐次式,降幂后最终化成y=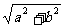 sin
(ωx+
sin
(ωx+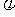 )+k的形式,二是化成某一个三角函数的二次三项式。本题(1)还可以解法如下:当cosx=0时,y=1;当cosx≠0时,y=
)+k的形式,二是化成某一个三角函数的二次三项式。本题(1)还可以解法如下:当cosx=0时,y=1;当cosx≠0时,y= +1=
+1=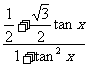 +1
+1
化简得:2(y-1)tan2x-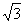 tanx+2y-3=0
tanx+2y-3=0
∵tanx∈R,∴△=3-8(y-1)(2y-3) ≥0,解之得: ≤y≤
≤y≤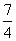
∴ymax=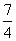 ,此时对应自变量x的值集为{x|x=kπ+
,此时对应自变量x的值集为{x|x=kπ+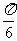 ,k∈Z}
,k∈Z}
例9、已知函数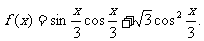
(Ⅰ)将f(x)写成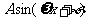 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
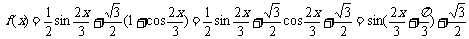
由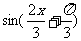 =0即
=0即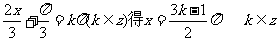
即对称中心的横坐标为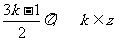
(Ⅱ)由已知b2=ac
 即
即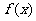 的值域为
的值域为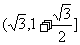 .
.
综上所述,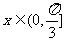 ,
,
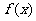 值域为
值域为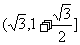 .
.
说明:本题综合运用了三角函数、余弦定理、基本不等式等知识,还需要利用数形结合的思想来解决函数值域的问题,有利于培养学生的运算能力,对知识进行整合的能力。
例10、设二次函数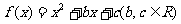 ,已知不论
,已知不论 为何实数恒有
为何实数恒有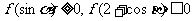 .
.
(1)
求证: ;
;
(2)
求证: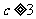 ;
;
(3)
若函数 的最大值为8,求
的最大值为8,求 的值.
的值.
(1)
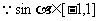 ,
, 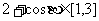 ,
,
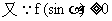 ,
, 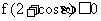 恒成立.
恒成立.
 ,
, 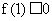 ,
即
,
即  恒成立.
恒成立.
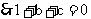 ,
即
,
即 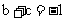 .
.
(2)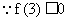 ,
, 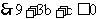 ,
,  ,
, 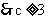 .
.
(3)由题意可知:  ,
,
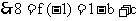 ①,
①,  ② ,
② ,
由 ① ,② 可得 b = 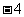 ,c = 3 .
,c = 3 .
说明:赋值法在解决有关恒成立问题时经常用到,利用函数的单调性往往能使问题得以顺利解决。
例11、已知函数
(1) 求函数y的最大值,并求此时x的值.
(2)
该函数的图象可由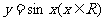 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
解:(1) 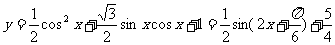 ,
,
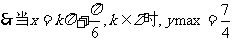 ;
;
(2)将函数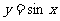 的图象依次进行如下变换:
的图象依次进行如下变换:
① 把函数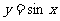 的图象向左平移
的图象向左平移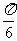 ,得到函数
,得到函数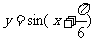 的图象;
的图象;
② 把得到的图象上各点横坐标缩短到原来的 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数
 的图象;
的图象;
③ 把得到的图象上各点纵坐标缩短到原来的 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数
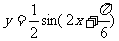 的图象;
的图象;
④把得到的图象向上平移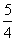 个单位长度,得到函数
个单位长度,得到函数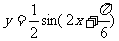 +
+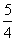 的图象;
的图象;
综上得函数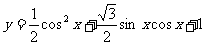 的图象.
的图象.
说明:图象变换是否熟练、准确是解决三角函数问题的关键,要求学生要熟练掌握。
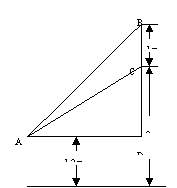
例12、化工厂的主控制表盘高1米,表盘底边距地面2米,问值班人员坐在什么位置上表盘看得最清楚?(设值班人员坐在椅子上时,眼睛距地面1.2米).
解:如图,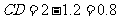 ,设
,设 ,则
,则
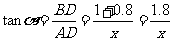 ,
,
 ,
,
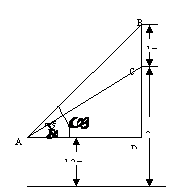
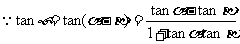 ,
,
 ,
,
当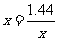 ,即
,即 时,
时,
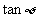 达到最大值
达到最大值 ,
,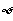 是锐角,
是锐角,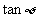 最大时,
最大时,
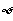 也最大,所以值班人员看表盘最清楚的位置为
也最大,所以值班人员看表盘最清楚的位置为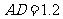 米.
米.
说明:欲在表盘看得清楚,人眼距表盘水平距离AD应使视角达到最大。合理利用角的关系,建立目标函数,是本题的关键。
例13、平面直角坐标系有点
(1)
求向量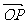 和
和 的夹角
的夹角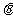 的余弦用
的余弦用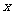 表示的函数
表示的函数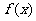 ;
;
(2)
求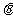 的最值.
的最值.
解:(1)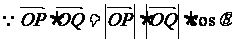 ,
,
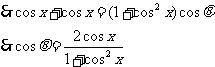
即 

(2)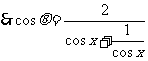 , 又
, 又 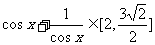 ,
,
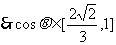 ,
, 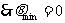 ,
, 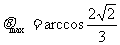 .
.
说明:三角函数与向量之间的联系很紧密,解题时要时刻注意。
例14、已知:定义在 上的减函数
上的减函数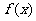 ,使得
,使得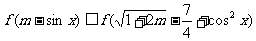 对一切实数
对一切实数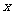 均成立,求实数
均成立,求实数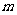 的范围.
的范围.
解:由题意可得
 ,
,
即 
 ,
,
又
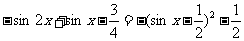 ,
,

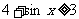 ,
,

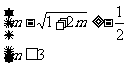 ,
, 
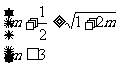 ,
,

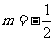 , 或
, 或
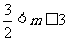 .
.
说明:利用三角函数的值域来求解变量的取值范围,是较为常见的解题思路,在利用单调性列出不等式时,不能忘记函数的定义域。
7.三角函数的单调性
“正切函数f (x)
= tan x,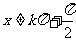
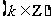 是定义域上的增函数”,是否正确.
是定义域上的增函数”,是否正确.
分析:我们按照函数单调性的定义来检验一下:
任取 ,
,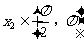 ,显然x1<x2,但f
(x1 )>0>f
(x2 ),与增函数的定义相违背,因此这种说法是不正确的.
,显然x1<x2,但f
(x1 )>0>f
(x2 ),与增函数的定义相违背,因此这种说法是不正确的.
观察图象可知:在每一个区间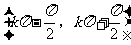
 上,f (x ) = tan x都是增函数,但不能说f (x ) = tan x在其定义域上是增函数.
上,f (x ) = tan x都是增函数,但不能说f (x ) = tan x在其定义域上是增函数.
6.三角函数的奇偶性
“函数y = sin (x+φ) (φ∈R)不可能是偶函数”.是否正确.
分析:当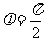 时,
时, ,这个函数显然是偶函数.因此,这个判断是错误的.我们容易得到如下结论:
,这个函数显然是偶函数.因此,这个判断是错误的.我们容易得到如下结论:
① 函数y = sin (x+φ)是奇函数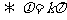
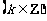 .
.
② 函数y = sin (x+φ)是偶函数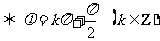 .
.
③ 函数y =cos (x+φ)是奇函数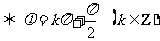 .
.
④ 函数y = cos (x+φ)是偶函数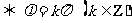 .
.
5. 三角函数的图象的掌握体现在:把握图象的主要特征(顶点、零点、中心、对称轴、单调性、渐近线等);应当熟练掌握用“五点法”作图的基本原理以及快速、准确地作图.
4. 单位圆中的三角函数线是三角函数值的几何表示,四种三角函数y = sin x、y = cos x、y = tan x、y = cot x的图象都是“平移”单位圆中的三角函数线得到的,因此应熟练掌握三角函数线并能应用它解决一些相关问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com