
6.(06四川)直线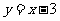 与抛物线
与抛物线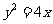 交于
交于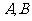 两点,过
两点,过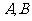 两点向抛物线的准线作垂线,垂足分别为
两点向抛物线的准线作垂线,垂足分别为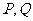 ,则梯形
,则梯形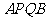 的面积为_________ .
的面积为_________ .
5. 若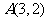 ,F是抛物线
,F是抛物线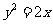 的焦点,P为抛物线上任意一点,则
的焦点,P为抛物线上任意一点,则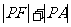 的最小值为___________,这时P点的坐标为____________ .
的最小值为___________,这时P点的坐标为____________ .
4. (06山东)过P(4,0)的直线与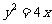 相交于
相交于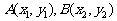 两点,则
两点,则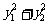 的最小值是 ____
的最小值是 ____
3.(06陕西)双曲线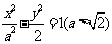 的两条渐近线的夹角为
的两条渐近线的夹角为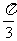 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)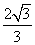 (B)
(B)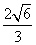 (C)
(C)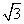 (D)2
(D)2
2.(06全国Ⅰ)双曲线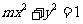 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则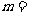 ( )
( )
A.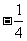 B.
B. C.
C.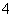 D.
D.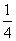
1. 已知定点A、B且|AB|=4,动点P满足|PA|-|PB|=3,则|PA|的最小值是 ( )
A.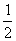 B.
B.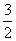 C.
C.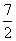 D.5
D.5
3.抛物线: ①.抛物线的定义:
②.开口向右、向左、向上、向下的抛物线及其标准方程的异同点:
相同点:1)原点在抛物线上; 2)对称轴为坐标轴;p值的意义表示焦点到准线的距离;
3)p>0为常数; 4)p值等于一次项系数绝对值的一半; 5)准线与对称轴垂直,垂足与焦点关于原点对称,它们与原点的距离等于一次项系数的绝对值的1/4,即2p/4=p/2.
不同点:
|
方程 |
对称轴 |
开口方向 |
焦点位置 |
|
y2=2px |
x轴 |
向右 |
x轴正半轴上 |
|
y2= -2px(p>0) |
x轴 |
向左 |
x轴负半轴上 |
|
x2=2py(p>0) |
y轴 |
向上 |
y轴正半轴上 |
|
x2= -2py(p>0) |
y轴 |
向下 |
y轴负半轴上 |
2.双曲线: ①. 双曲线的定义:
②双曲线的标准方程:
③双曲线的几何性质: :以标准方程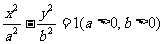 为例.
为例.
1)范围:|x|≥a;即x≥a,x≤-a. 2)对称性:对称轴为x=0,y=0;对称中心为O(0,0).
3)顶点:A1(-a,0),A2(a,0)为双曲线的两个顶点;线段A1A2叫双曲线的实轴,B1B2叫双曲线的虚轴,其中B1(0,b),B2(0,b).|A1A2|=2a,|B1B2|=2b.
4)渐近线:双曲线渐近线的方程为y=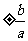 x; 5)准线:x=
x; 5)准线:x=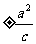 ;
6)离心率:e=
;
6)离心率:e=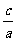 ,e>1.
,e>1.
④.等轴双曲线:x2-y2=±a2,实轴长等于虚轴长,其渐近线方程为y=±x,离心率e=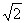
1.椭圆:①.椭圆的定义:
②椭圆的标准方程:
③椭圆的参数方程:
④椭圆的几何性质:以标准方程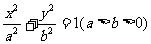 为例:
为例:
1)范围:|x|≤a,|y|≤b; 2)对称性:对称轴x=0,y=0,对称中心为O(0,0);
3)顶点A(a,0),A′(-a,0),B(0,b),B′(0,-b);长轴|AA′|=2a,短轴|BB′|=2b;
4)离心率:e=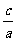 ,0<e<1; 5)准线x=±
,0<e<1; 5)准线x=±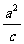 ; 6)焦半径:|PF1|=a+ex,|PF2|=a-ex,其中P(x,y)是椭圆上任意一点.
; 6)焦半径:|PF1|=a+ex,|PF2|=a-ex,其中P(x,y)是椭圆上任意一点.
9. 某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.电脑单价A型:6000元;A型:6000元;B型:4000元;C型:2500元;D型:4000元;E型:2000元;
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台,恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com