
20.(本小题满分13分)三个城市长沙、株洲、湘潭分别位于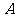 ,
,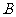 ,
,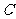 三点处(如右图),且
三点处(如右图),且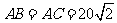 km,
km,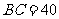 km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与
km.今计划合建一个货运中转站,为同时方便三个城市,准备建在与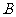 、
、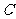 等距离的
等距离的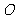 点处,并修建道路
点处,并修建道路 .记修建的道路的总长度为
.记修建的道路的总长度为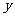 km.
km.
(1)设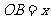 (km),或
(km),或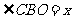 (rad).请你选择用其中的某个
(rad).请你选择用其中的某个 ,将
,将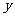 表示为
表示为 的函数;
的函数;
(2)由(1)中建立的函数关系,确定货运中转站的位置,使修建的道路的总长度最短.
19.(本小题满分13分)
已知二次函数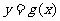 的导函数的图像与直线
的导函数的图像与直线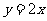 平行,且
平行,且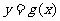 在
在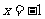 处取得极小值
处取得极小值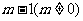 .设
.设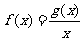 .
.
(1)若曲线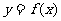 上的点
上的点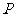 到点
到点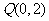 的距离的最小值为
的距离的最小值为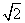 ,求
,求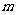 的值;
的值;
(2)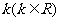 如何取值时,函数
如何取值时,函数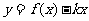 存在零点,并求出零点.
存在零点,并求出零点.
解:(1)依题可设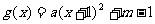 (
(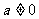 ),则
),则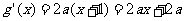 ;
;
又 的图像与直线
的图像与直线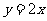 平行
平行 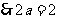

 ,
, 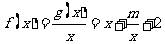 ,
,
设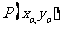 ,则
,则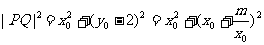 21世纪教育网
21世纪教育网 

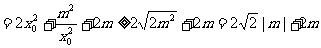
当且仅当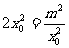 时,
时,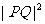 取得最小值,即
取得最小值,即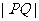 取得最小值
取得最小值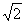
当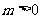 时,
时,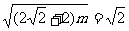 解得
解得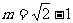
当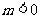 时,
时,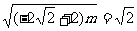 解得
解得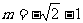
(2)由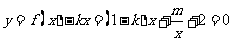 (
(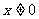 ),得
),得
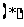
当 时,方程
时,方程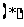 有一解
有一解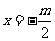 ,函数
,函数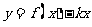 有一零点
有一零点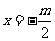 ;
;
当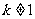 时,方程
时,方程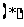 有二解
有二解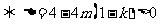 ,若
,若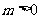 ,
,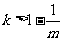 ,
,
函数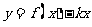 有两个零点
有两个零点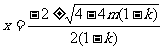 ,即
,即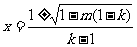 ;
;
若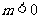 ,
,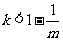 ,函数
,函数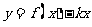 有两个零点
有两个零点 ,即
,即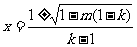 ;
;
当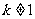 时,方程
时,方程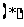 有一解
有一解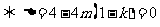 ,
, 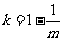 ,
,
函数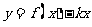 有一零点
有一零点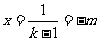
综上,当 时, 函数
时, 函数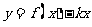 有一零点
有一零点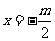 ;
;
当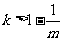 (
(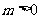 ),或
),或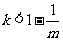 (
(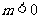 )时,函数
)时,函数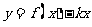 有两个零点
有两个零点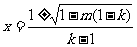 ;
;
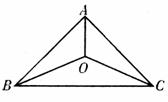 当
当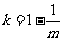 时,函数
时,函数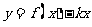 有一零点
有一零点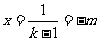 .
.
18、(1)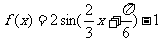
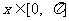
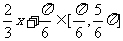
∴当 ∴
∴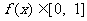

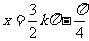 ,对称中心
,对称中心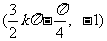
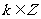
(2)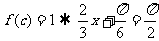
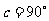
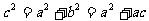
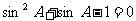 ,
,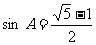
18. (本小题满分12分)若
(本小题满分12分)若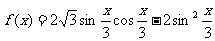
(1) 求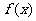 的对称中心坐标及f(x)在
的对称中心坐标及f(x)在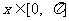 上的值域;
上的值域;
(2) 在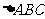 中,A、B、C所对边分别为a、b、c,若
中,A、B、C所对边分别为a、b、c,若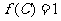 ,且
,且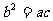 ,求
,求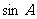 .
.
17.解:由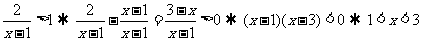
设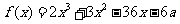 ,
,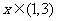 .
.
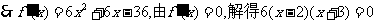
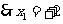 ,或
,或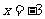 (舍去).
(舍去).
又当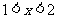 时,
时,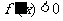 ,
,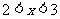 时,
时,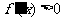 ,
,
 在
在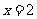 处取得最小值
处取得最小值 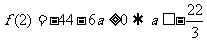 .
.
17.(本小题满分12分)若对满足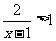 的任意实数
的任意实数 ,使得不等式
,使得不等式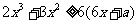 恒成立,求实数
恒成立,求实数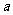 的取值范围.
的取值范围.
16.(本小题满分12分) 在△ABC中,角A、B、C的对边分别是a、b、c,且A为锐角,
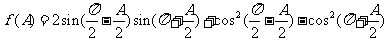
⑴求f(A)的最小值;
⑵若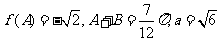 ,求b的大小.
,求b的大小.
解:(1)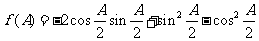
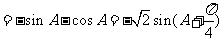
∵A为锐角,∴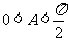 ,∴
,∴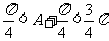 ,
,
∴当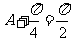 时,
时,
(2)由题意知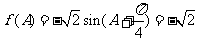 ,∴
,∴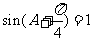 .
.
又∵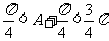 ,∴
,∴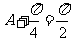 ,∴
,∴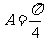 ,
,
又∵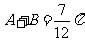 ,∴
,∴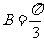 ,
,
由正弦定理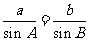 得
得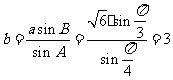 .
.
15.已知: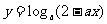 在
在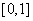 上是单调递减的,则函数
上是单调递减的,则函数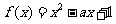 在
在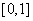 上的最大值是 1 。
上的最大值是 1 。
14. 已知tan(A-B)=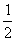 , tanB=
, tanB=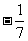 ,且A,B
,且A,B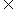 (0,
(0,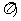 ,则2A-B的值为__
,则2A-B的值为__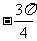 _________
_________
13.已知函数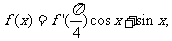 则
则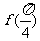 的值为 1 .
的值为 1 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com