
22._______ , I’ll wait for you to have dinner together. Be back as early as possible.
A. However late it is B. No matter how it is late
C. However it is late D. No matter how late is it
第一节:单项填空(共15小题,每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21.If I drive in this city myself, I’ll probably get lost as I haven’t got very good sense of ________direction.
A.a; 不填 B.the; 不填 C.a; the D.the; a
20.(本小题满分14分)
设函数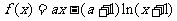 ,其中
,其中 ,求
,求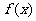 的单调区间.
的单调区间.
解: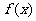 的定义域是
的定义域是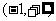
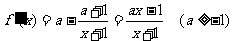
(1)当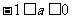 时,
时,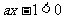 ,此时
,此时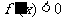 ,故
,故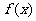 在
在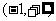 是减函数;
是减函数;
(2)当 时,令
时,令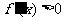 得
得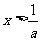 ,
,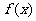 在
在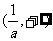 是增函数,
是增函数,
令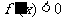 得
得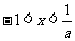 ,
,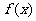 在
在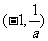 是减函数。
是减函数。
综上当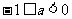 时,
时,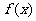 在
在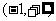 是减函数;
是减函数;
当 时,
时,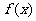 在
在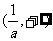 是增函数,在
是增函数,在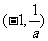 是减函数。
是减函数。
19.(本小题满分12分)
已知函数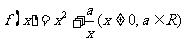
(1)判断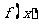 的奇偶性(直接写出你的结论)
的奇偶性(直接写出你的结论)
(2)若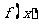 在
在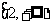 是增函数,求实数
是增函数,求实数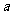 的范围
的范围
解:(1)当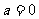 时,
时,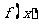 为偶函数;
为偶函数;
当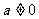 时,
时,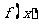 为非奇非偶函数。
为非奇非偶函数。
(2)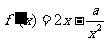
依题意,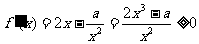 在
在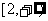 上恒成立,
上恒成立,
即 在
在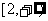 上恒成立。
上恒成立。
只需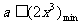
而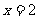 时,
时,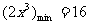 ,故
,故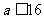
18.(本小题满分14分)
解关于实数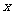 的不等式
的不等式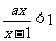 ,
,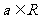
解:(1)当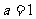 时,原不等式等价于
时,原不等式等价于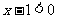 ,即
,即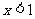 ,故原不等式的解集为
,故原不等式的解集为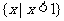
(2)当 时,原不等式等价于
时,原不等式等价于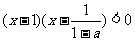 即
即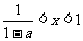 ,故原不等式的解集为
,故原不等式的解集为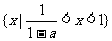
(3)当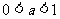 时,原不等式等价于
时,原不等式等价于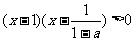 即
即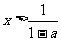 或
或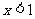 ,故原不等式的解集为
,故原不等式的解集为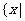
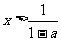 或
或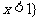
(4)当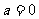 时,原不等式等价于
时,原不等式等价于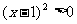 ,即
,即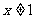 ,故原不等式的解集为
,故原不等式的解集为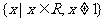
(5)当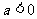 时,原不等式等价于
时,原不等式等价于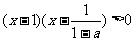 ,即
,即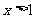 或
或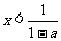 ,故原不等式的解集为
,故原不等式的解集为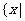
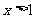 或
或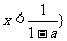
17.(本小题满分14分)
已知函数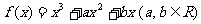 的图象过点
的图象过点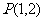 ,且在点
,且在点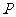 处的切线斜率为8.
处的切线斜率为8.
(Ⅰ)求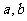 的值; (Ⅱ)求函数
的值; (Ⅱ)求函数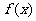 的单调区间;
的单调区间;
(Ⅰ)解:∵函数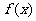 的图象过点
的图象过点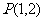 ,
,
∴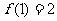 .
.
∴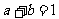 . ①
. ①
又函数图象在点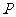 处的切线斜率为8,
处的切线斜率为8,
∴ 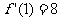 ,
,
又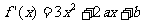 ,
,
∴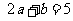 . ②
. ②
解由①②组成的方程组,可得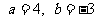 .
.
(Ⅱ)由(Ⅰ)得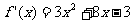 ,
,
令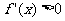 ,可得
,可得 ;
;
令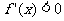 ,可得
,可得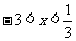 .
.
∴函数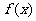 的单调增区间为
的单调增区间为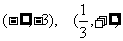 ,减区间为
,减区间为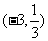 .
.
16.(本小题满分14分)已知函数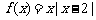 .
.
(Ⅰ)写出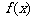 的单调区间;
的单调区间;
(Ⅱ)解不等式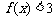 ;
;
(Ⅲ)设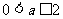 ,求
,求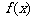 在
在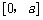 上的最大值.
上的最大值.
(Ⅰ)解: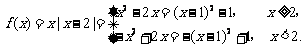
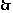
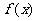 的单调递增区间是
的单调递增区间是 ; 单调递减区间是
; 单调递减区间是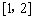 .
.
(Ⅱ)解:
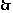 不等式
不等式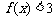 的解集为
的解集为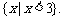
(Ⅲ)解:(1)当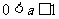 时,
时,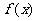 是
是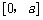 上的增函数,此时
上的增函数,此时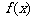 在
在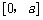 上的最大值是
上的最大值是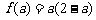
(2)当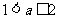 时,
时,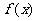 在
在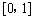 上是增函数,在
上是增函数,在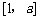 上是减函数,此时
上是减函数,此时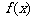 在
在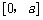 上的最大值是
上的最大值是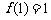 ;
;
综上,当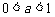 时,
时,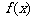 在
在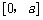 上的最大值是
上的最大值是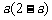 ;当
;当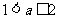 时,
时,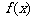 在
在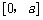 上的最大值是
上的最大值是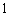 。
。
15.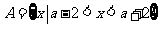 ,
,
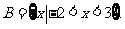 若
若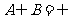 ,应令
,应令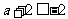 或
或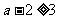
解得 或
或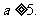
故使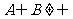 的实数
的实数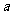 的取值范围为
的取值范围为 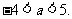
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com