(二)选做题(14-15题，考生只能从中选做一题)

14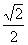．[解析]点(1，0)的直角坐标为(1，0)，直线的直角坐标方程为x+y-2=0，所以点到直线的距离为．

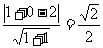[链接高考]极坐标的问题主要是把它转化为直角坐标中来解决，当然也可以在极坐标

系中解决．

15．3[解析]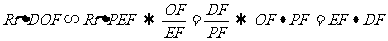；又相交弦定理得：DFFE=BFAF，所以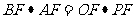；设OF=x,BF=2-x,AF=2+x,PF=4-x代入可求得x=1,即PF=3．

[链接高考]本小题主要考查圆中相交弦、圆周角等几何知识，同时也考查了方程的思

想.

(一)必做题(11-13题)

11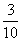．、2.2[解析]从中任意选1名学生，他参加活动次数为3的概率是:，

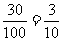由统计图知该文学社学生参加活动的人均次数为:．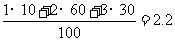

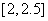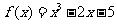12．[解析]令，则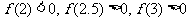，可知下一个有解区间为．

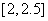13．①②③④[解析]由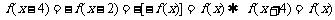，故①正确；

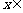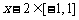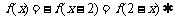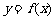由[1，3]得，所以，故②正确；由已知得函数的图象关于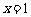对称，故正确③；由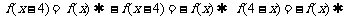函数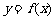的图象关于点(2，0)对称，故④正确．

[链接高考]本题是对抽象函数的周期性、对称性等性质的综合考查。对这类问题可以根据已知条件作出函数图象，从而有助问题的解决．

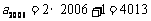10．D．[解析]若△ABC内只有1个点，则共有3个小三角形，有2个点，则共有5个小三角形，有3个点，则共有7个小三角形，由此可知小三角形的个数构成以3为首项，以2为公差的等差数列，通项公式为，所以，，故选D．

[链接高考]本题是数列的应用题，考查对问题的观察、转化、合情推理的能力．

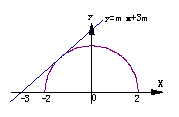
9．A．[解析]如图当直线与半圆相切时，易得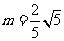，当切线绕点(－3,0)

沿顺时针旋转到与x轴重合时，都能保证直线与半圆有两个交点，

故答案选A.

8．C．[解析]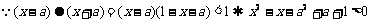对任意实数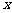都成立， .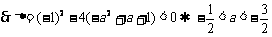

[链接高考]近年各地的高考常出现这类重新定义一种新的运算，并由此综合某些知识点进行考查，解决的关键是把新的定义运算转化为旧的运算模式.

7．D．[解析]由函数的导数的意义可知，原函数图象从左到右是增→增→减→增，对应的导数的符号 为正→正→负→正，故选D．

[链接高考]对导数部分的考查近年高考有加大的趋势，本题是对导数的几何意义的考查.

6．C．[解析]①中的反例是“墙角”，②③是正确的．

[链接高考]本小题考查立几中线面、面面的关系，是新课程的要求，做此类问题要讲究方法，充分利用笔和纸做模型来帮助．

5．A．[解析]由流程图可得出此函数既是奇函数又存在零点，因此选A．

[链接高考]本小题主要考查框图知识和数列知识,以及分析问题和解决问题的能力. 算法初步是高考新增的考点.近两年每年都有一道小题,常与函数、数列等知识进行小综合来考查,估计以后的考查形式不会有大的变化．

4．B．[解析]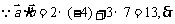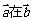方向上的投影为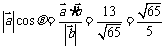，故选B．

[链接高考]本题是考查向量中一个向量在另一个向量的投影的概念。向量部分是每年高考必考的内容，而本题是考查一个容易忽略的概念，值得大家留意．

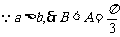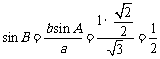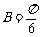3．B．[解析]，由正弦定理得，所以，故选B．

[链接高考]正(余)弦定理是解三角形的基础，也是高考必考的内容。本题是正确运用正弦定理的一个应用，并注意运用大边对大角的性质得出只有一个解的情况．