19．(本小题满分12分)

　　　 一辆汽车在某段路程中的行驶速度与时间的关系如右图：

　 (1)求图中阴影部分的面积，并说明所求面积的实际意义；

　 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km，试建立汽车行驶这段路程时汽车里程表读数S和时间t的函数解析式。

18．(本小题10分)

　　　 指数函数的图象如图所示。

　 (1)在已知图象的基础上画出指数函数的图象；

　 (2)求的顶点的横坐标的取值范围。

17．(本小题10分)

　　　 已知集合

　 (1)求A∪B；(C_RA)∩B；

　 (2)若A∩B≠，求的取值范围。

16．若一次函数有一个零点2，那么函数的零点是　　　 。

15．已知幂函数的图象过点，则=　　　　　 。

14．函数的定义域为　　　　 。

13．求值：=　　　　　　　 ，=　　　　　　　　 。

12．某林区的森林蓄积量每年比上一年平均增长10.4%，要增长到原来的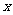倍，需经过y年，则函数的图象大致为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

11．下表显示出函数值y随自变量x变化的一组数据，由此判断它最可能的函数模型是(　　 )

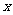	4	5	6	7	8	9	10
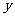	15	17	19	21	23	25	27

　　　 A．一次函数模型　　　　　　　　　　　　　　　　　　 B．二次函数模型

　　　 C．指数函数模型　　　　　　　　　　　　　　　　　　 D．对数函数模型

9．函数在[0，1]上的最大值与最小值的和为3，则=　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　　　　　　　 B．2　　　　　　　　　　　　 C．4　　　　　　　　　　　 D．

　　　 A．3.71　　　　　　　　　 B．3.97　　　　　　　　　 C．4.24　　　　　　　　　 D．4.77