
4.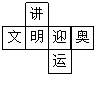 (08长沙)如图是每个面上都有一个汉字的正方体
(08长沙)如图是每个面上都有一个汉字的正方体
的一种展开图,那么在正方体的表面,与“迎”相
 对的面上的汉字是( )
对的面上的汉字是( )
A.文 B.明 C.奥 D.运
3.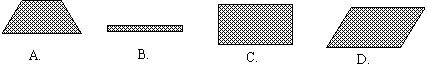 (08贵阳)在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是( )
(08贵阳)在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是( )
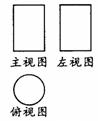
2. (08深圳) 如图,圆柱的左视图是( )

1.(08福州)如图所示的物体是一个几何体,其主视图是( )

21. [解析]证明:显然,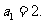 ……………………………………………..…1分
……………………………………………..…1分
下面考虑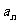 与
与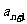 的关系.
的关系.
奇数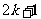 的最大奇数因子是
的最大奇数因子是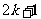 ;形如
;形如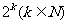 的数的最大奇数因子是1.……………………………………………………………….3分
的数的最大奇数因子是1.……………………………………………………………….3分
由于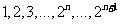 中各项的最大奇数因子之和为
中各项的最大奇数因子之和为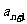 ,则
,则 ,其中
,其中 是数列
是数列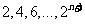 中各项最大奇数因子之和,它等于
中各项最大奇数因子之和,它等于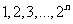 中各项的最大奇数因子之和.所以有
中各项的最大奇数因子之和.所以有
 . ………………………5分
. ………………………5分
因此,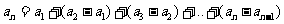
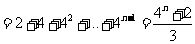 , ………………………………….…8分
, ………………………………….…8分
从而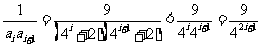 ,…………….……………11分
,…………….……………11分
故,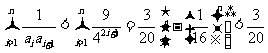 .…………………………14分
.…………………………14分
20.[解析](I) 设椭圆方程为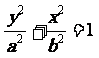 (
(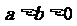 ),∵椭圆过点P
),∵椭圆过点P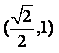 ,则由椭圆的定义知
,则由椭圆的定义知
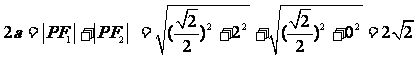 ……….….1分
……….….1分
所以,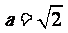 ,
,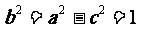 ,……. …………………..2分
,……. …………………..2分
椭圆C的方程为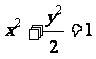 ………………………….…………4分
………………………….…………4分
(II)解法一:
若直线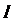 与x轴重合,则以AB为直径的圆是
与x轴重合,则以AB为直径的圆是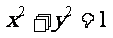 ;
;
若直线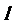 垂直于x轴时,则以AB为直径的圆是
垂直于x轴时,则以AB为直径的圆是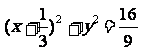 . ………………………………………..……5分
. ………………………………………..……5分
由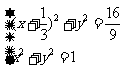 解得
解得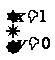 ,所以两圆相切于点(1,0).
,所以两圆相切于点(1,0).
因此,如果存在点T满足条件,则该点只能是(1,0).….……6分
下面证明T(1,0)就是所求的点.
若直线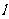 垂直于x轴时,
垂直于x轴时,
则以AB为直径的圆经过点(1,0);
若直线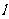 不垂直于x轴时,可设直线
不垂直于x轴时,可设直线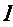 :
: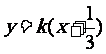
由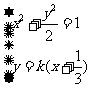 ,整理得
,整理得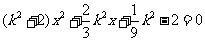 .………..……8分
.………..……8分
记A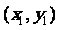 、B(
、B(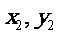 ),则
),则 .…..…………..…9分
.…..…………..…9分
又因为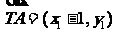 ,
,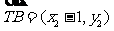 ,
,
则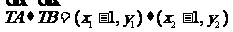 =
=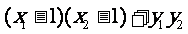
=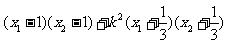 =
=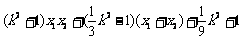 ..10分
..10分
=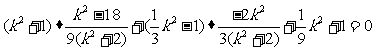 .………………...13分
.………………...13分
所以,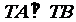 ,即以AB为直径的圆恒过定点T(1,0),
,即以AB为直径的圆恒过定点T(1,0),
故平面上存在一个定点T(1,0)满足题设条件.………….…..…14分
解法二:(I)由已知c=1,设椭圆方程为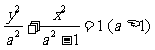 .……1分
.……1分
因为点P在椭圆上,则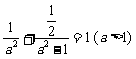 ,解得
,解得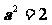 ,……..……2分
,……..……2分
所以椭圆方程为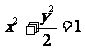 .…………………………………….……4分
.…………………………………….……4分
(II)如果存在定点T(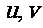 )满足条件.
)满足条件.
若直线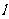 垂直于x轴时,
垂直于x轴时,
则以AB为直径的圆经过点(1,0);…………………………..…5分
若直线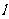 不垂直于x轴时,可设直线
不垂直于x轴时,可设直线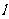 :
: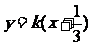 .
.
由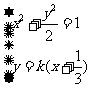 ,整理得
,整理得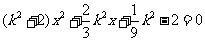 .………………. 6分
.………………. 6分
记A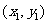 、B(
、B(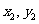 ),则
),则 .…………………..…7分
.…………………..…7分
∵又因为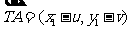 ,
,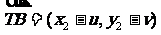 ,
,
则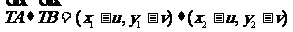 =
=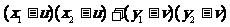
=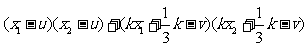
=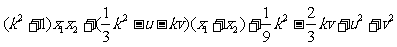 ………..8分
………..8分
=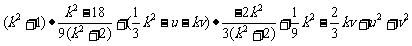
=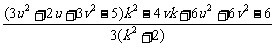 .……………………….…9分
.……………………….…9分
当且仅当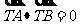 恒成立时,以AB为直径的圆恒过点
恒成立时,以AB为直径的圆恒过点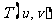 .
.
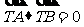 恒成立等价于
恒成立等价于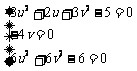 ,
,
解得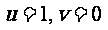 .……………………………………….…….12分
.……………………………………….…….12分
所以当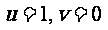 时,无论直线
时,无论直线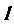 如何转动,以AB为直径的圆恒过定点
如何转动,以AB为直径的圆恒过定点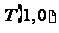 .
.
故平面上存在一个定点T(1,0)满足题目条件.…………14分
19. [解析](Ⅰ)证明:如右图,过点A在平面A1ABB1内作
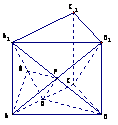 AD⊥A1B于D,则
AD⊥A1B于D,则
由平面A1BC⊥侧面A1ABB1,且平面A1BC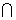 侧面A1ABB1=A1B,得
侧面A1ABB1=A1B,得
AD⊥平面A1BC,又BC 平面A1BC,
平面A1BC,
所以AD⊥BC. ……………………………………………………...2分
因为三棱柱ABC-A1B1C1是直三棱柱,
则AA1⊥底面ABC,
所以AA1⊥BC.……………………………………………..……..…3分
又AA1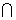 AD=A,从而BC⊥侧面A1ABB1,
AD=A,从而BC⊥侧面A1ABB1,
又AB 侧面A1ABB1,故AB⊥BC. ………………………..…...4分
侧面A1ABB1,故AB⊥BC. ………………………..…...4分
(Ⅱ)解法1:连接CD,则由(Ⅰ)知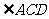 是直线AC与平面A1BC所成的角,……………………………………….………………...6分
是直线AC与平面A1BC所成的角,……………………………………….………………...6分
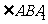 是二面角A1-BC-A的平面角,即
是二面角A1-BC-A的平面角,即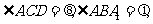
于是在Rt△ADC中,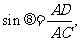 在Rt△ADB中,
在Rt△ADB中,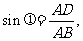 …...8分
…...8分
由AB<AC,得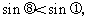 ………………………………….……...11分
………………………………….……...11分
又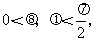 所以
所以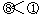 .…………………………………………....13分
.…………………………………………....13分
解法2:由(Ⅰ)知,以点B为坐标原点,以BC、BA、BB1所在的直线分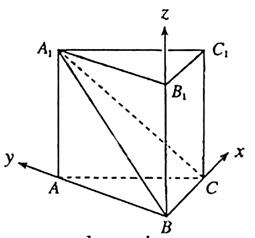 别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,设AA1=a,AC=b,
别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,设AA1=a,AC=b,
AB=c,则 B(0,0,0), A(0,c,0), 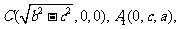 ……………....5分
……………....5分
于是
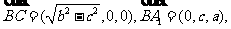
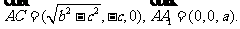 .………………………..………...6分
.………………………..………...6分
设平面A1BC的一个法向量为n=(x,y,z),则
由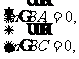 得
得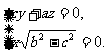
可取n=(0,-a,c),于是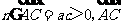 与n的夹角
与n的夹角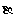 为锐角,则
为锐角,则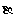 与
与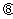 互为余角.
互为余角.
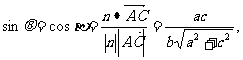 …………………………....……8分
…………………………....……8分
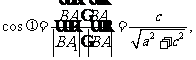 所以
所以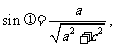 ………..………..11分
………..………..11分
于是由c<b,得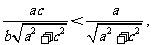
即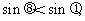 又
又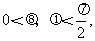 所以
所以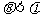 .……………………...13分
.……………………...13分
18. [解析](1)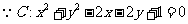
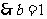 时,点
时,点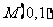 在圆上.又
在圆上.又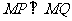
,圆心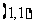 在直线直线
在直线直线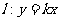 上,故
上,故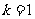 . ………………………..2分
. ………………………..2分
(2)设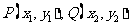 .
.
联立方程组,
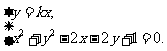
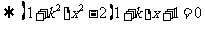 ,
,
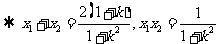 .………………………………………………………. 4分
.………………………………………………………. 4分
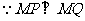
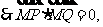 即
即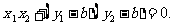
又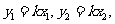
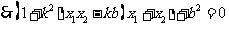 ,………………. 6分
,………………. 6分
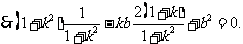
当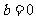 时,此式不成立,
时,此式不成立,
从而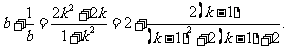 …………………………. 9分
…………………………. 9分
又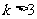 ,令
,令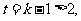
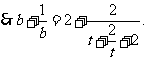 令函数
令函数 当
当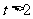 时,
时,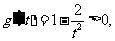
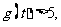 从而
从而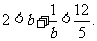 ……………………………… 11分
……………………………… 11分
解此不等式。可得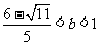 或
或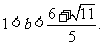 .…………………… 13分
.…………………… 13分
17.[解析](Ⅰ)设甲、乙两人参加交通知识考试合格的事件分别为A、B,则
P(A)=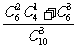 =
=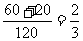 ,P(B)=
,P(B)=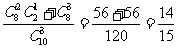 . ………3分
. ………3分
因为事件A、B相互独立,
∴甲、乙两人考试均合格的概率为
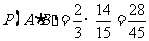 . ……………………5分
. ……………………5分
答:甲、乙两人考试均合格的概率为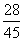 . …………………………6分
. …………………………6分
(Ⅱ)依题意,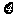 =0,1,2,3,………………7分
=0,1,2,3,………………7分
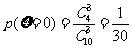 ,
, 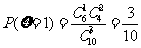 ,
,
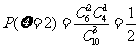 ,
,
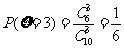 . ……………………………9分
. ……………………………9分
甲答对试题数ξ的概率分布如下:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
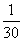 |
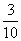 |
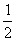 |
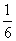 |
甲答对试题数ξ的数学期望

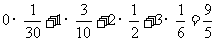 .
……………………13分
.
……………………13分
16.[解析](I)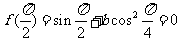 ,
,
则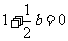 ,解得
,解得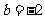 ;
-----------------------3分
;
-----------------------3分
所以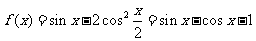 ,
,
则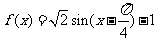 . --------------------------------5分
. --------------------------------5分
所以函数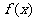 的最小正周期为
的最小正周期为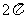 .…………………………6分
.…………………………6分
(I)由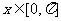 ,得
,得 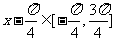 ,
,
则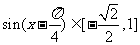 , -----------------------------------10分
, -----------------------------------10分
则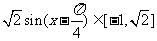 ,
,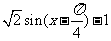
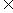
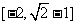 ,
,
所以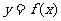 值域为
值域为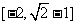 .……………………………………13分
.……………………………………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com