
2、甲、乙两人下棋,甲获胜的概率为30%,,两人下成和棋的概率为50%,那么甲不输棋的概率是
1、四面体的顶点和各棱的中点共10个点,
在其中取4个点,则这四个点不共面的概率
( )
A .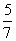 B.
B. 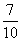 C.
C. 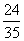 D.
D. 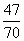
3、袋中装有大小相同且分别写有1、2、3、4、5五个号码的小球各一个,现从中有放回地任取三球,三个号码全不相同的概率为( )
A、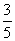 B、
B、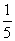 C、
C、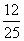 D、
D、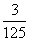
[经典范例]
例1 某射手在同一条件下进行射击结果如下表所示
|
射击次数 |
击中靶心的次数 |
击中靶心的频率 |
|
10 |
8 |
|
|
50 |
20 |
|
|
100 |
48 |
|
|
200 |
90 |
|
|
500 |
225 |
|
|
800 |
360 |
|
(1)计算表中各个击中靶心的频率;
(2)这个射手击中靶心的概率是多少?
(3)这个射手射击2000次估计击中靶心的次数为多少?
[解]
例2 袋中装有大小均匀分别写有1,2,3,4,5五个号码的小球各一个,现从中有放回地任取三个球,求下列事件的概率:
(1)所取的三个球号码完全不同;
(2)所取的三个球号码中不含4和5.
[解]
例3 一个各面都涂有色彩的正方体,被锯成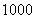 个同样大小的小正方体,将这些正方体混合后,从中任取一个小正方体,求:⑴有一面涂有色彩的概率;⑵有两面涂有色彩的概率;⑶有三面涂有色彩的概率.
个同样大小的小正方体,将这些正方体混合后,从中任取一个小正方体,求:⑴有一面涂有色彩的概率;⑵有两面涂有色彩的概率;⑶有三面涂有色彩的概率.
[解]
例4 9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为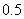 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种.
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种.
(Ⅰ)求甲坑不需要补种的概率;
(Ⅱ)求3个坑中恰有1个坑不需要补种的概率;
(Ⅲ)求有坑需要补种的概率.
(精确到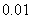 )
)
[解]
例5 一个盒中装有8只球,其中4红.3黑.1白,现从中取出2只球(无放回),
求:(1)全是红球或全是黑球的概率; (2)至少有一个红球的概率。
[解]
例6 甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6.本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响,求:
(Ⅰ) 前三局比赛甲队领先的概率;
(Ⅱ) 本场比赛乙队以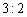 取胜的概率.
取胜的概率.
(精确到0.001)
[解]
追踪训练
2、从一堆产品(其中正品和次品都多于2个)中任取2个,其中:①恰有1件次品和恰有2件次品;②至少有1件次品和全是次品;③至少有1件正品和至少有1 件次品;④至少有1件次品和全是正品;上述事件中,是互斥事件的是( )
A ①④ B ②③ C ①②③ D ①②③④
1、下列事件中,属于随机事件的是 ( )
A. 掷一枚硬币一次,出现两个正面;
B、同性电荷互相排斥;
C、当a为实数时,|a|<0;
D、2009年10月1日天津下雨
3、在一条单行道上行进着一辆汽车,车长为4米,车宽为2米,汽车速度为36千米/小时,汽车车距为20米,有人突然从道旁某店内冲出,以2米/秒的速度垂直穿过街道,没有注意这辆汽车,试问:此人穿过街道未撞上汽车的概率为 。
2、从4双不同的鞋子中任取4只,则至少有2只配对的概率为 。
1、 某市派出甲、乙两支球队参加全省足球冠军赛.甲乙两队夺取冠军的概率分别是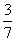 和
和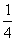 .试求该市足球队夺得全省足球冠军的概率.
.试求该市足球队夺得全省足球冠军的概率.
3、回答下列问题:
(1)甲、乙两射手同时射击一目标,甲的命中率为0.65,乙的命中率为0.60,那么能否得出结论:目标被命中的概率等于0.65+0.60=1.25,为什么?
(2)一射手命中靶的内圈的概率是0.25,命中靶的其余部分的概率是0.50,那么能否得出结论:目标被命中的概率等于0.25+0.50=0.75,为什么?
(3)两人各掷一枚硬币,“同时出现正面”的概率可以算得为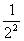 .由于“不出现正面”是上述事件的对立事件,所以它的概率等于
.由于“不出现正面”是上述事件的对立事件,所以它的概率等于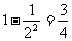 这样做对吗?说明道理.
这样做对吗?说明道理.
[解]
[经典范例]
例1 在(0,1)区间内任意取两实数,求它们的和大于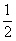 而小于
而小于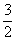 的概率.
的概率.
[解]
例2 假设一直角三角形的两直角边长都是0,1间的随机数,试求斜边长小于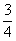 事件的概率.
事件的概率.
[解]
例3 从男女学生共有36名的班级中,任意选出2名委员,任何人都有同样的当选机会.如果选得同性委员的概率等于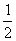 ,男女生相差几名?
,男女生相差几名?
[解]
例4 有三个人,每个人都以相同的概率被分配到四个房间中的每一间.试求(1)三个人都分配到同一房间的概率;(2)至少有两个人分配到同一房间的概率.
(点拨:∵三个人以同样的概率分配到每个房间,而三个人中每个人都可以分配到四个房间中的每一间,∴共有4×4×4=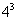 种方法.)
种方法.)
[解]
追踪训练
2、 向面积为S的△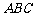 内任投一点P,则△
内任投一点P,则△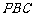 的面积小于
的面积小于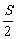 的概率为________.
的概率为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com