
3.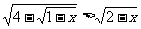 (
(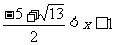 )s
)s
2.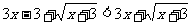

补充:解下列不等式
1.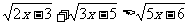
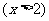
解 :要使不等式有意义必须:
原不等式可变形为 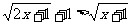 因为两边均为非负
因为两边均为非负
∴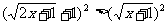 即
即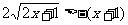
∵x+1≥0
∴不等式的解为2x+1≥0 即 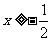
例五 解不等式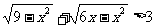
解:要使不等式有意义必须: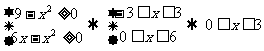
在0≤x≤3内 0≤ ≤3 0≤
≤3 0≤ ≤3
≤3
∴ >3-
>3- 因为不等式两边均为非负
因为不等式两边均为非负
两边平方得: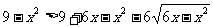 即
即 >x
>x
因为两边非负,再次平方: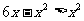 解之0<x<3
解之0<x<3
综合 得:原不等式的解集为0<x<3
例六 解不等式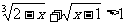
解:定义域 x-1≥0 x≥1
原不等式可化为: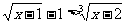
两边立方并整理得: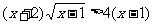
在此条件下两边再平方,
整理得: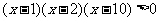
解之并联系定义域得原不等式的解为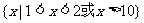
例三 解不等式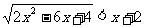
解:原不等式等价于
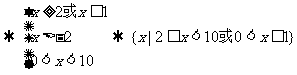
特别提醒注意:取等号的情况
例二 解不等式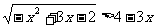
解:原不等式等价于下列两个不等式组得解集的并集:
Ⅰ: Ⅱ:
Ⅱ: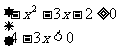
解Ⅰ: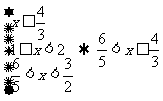 解Ⅱ:
解Ⅱ: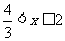
∴原不等式的解集为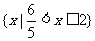
例一 解不等式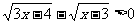
解:∵根式有意义 ∴必须有: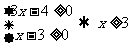
又有 ∵ 原不等式可化为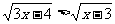
两边平方得: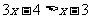 解之:
解之: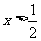
∴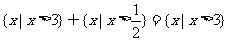
20.(本小题满分14分)
设函数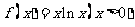 : (1)求函数
: (1)求函数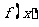 的最小值.
的最小值.
(2)设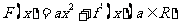 ,讨论函数
,讨论函数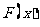 的单调性.
的单调性.
(3)当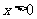 时,证明:
时,证明: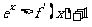 .
.
广东省湛江市麻章一中2009-2010学年度10月月考
19. (本小题满分14分)
(本小题满分14分)
如图,在四棱锥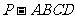 中,四边形
中,四边形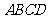 是正方形,
是正方形,
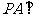 平面
平面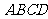 ,
,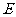 是
是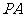 上的一点,
上的一点,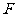 是
是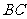 的中点.
21世纪教育网
的中点.
21世纪教育网
(1)求证: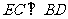 ;
;
(2)若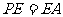 ,求证:
,求证: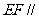 平面
平面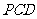 .
.
18.(本小题满分14分)
数列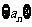 中,其前
中,其前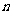 项和为
项和为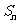 ,满足
,满足 ,数列
,数列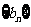 满足
满足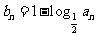 ,
,
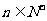 .(1)求数列
.(1)求数列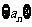 ,
,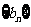 的通项公式. (2)设数列
的通项公式. (2)设数列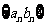 的前
的前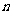 项和为
项和为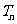 ,求
,求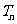 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com