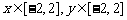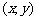2、若,则点在圆面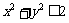内的概率是多少?

解：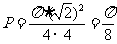

1、求例1中(2)的概率．

解：由例1(2)分析可知：

．

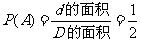2、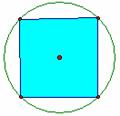我们可以通过实验计算圆周率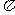的近似值．实验如下：向如图所示的圆内投掷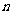个质点，计算圆的内接正方形中的质点数为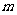，由几何概型公式可知：，

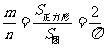即　 ．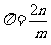

追踪训练

1、几何概型的意义也可以这样理解： 向区域G中任意投掷一个点M，点M落在G内的部分区域g”的概率P定义为：g的度量与G的度量之比，即：

．

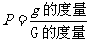3．几何概型的概率：

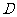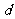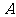一般地，在几何区域中随机地取一点，记事件＂该点落在其内部一个区域内＂为事件，则事件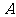发生的概率．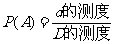

说明：(1)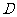的测度不为；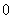

(2)其中＂测度＂的意义依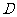确定，当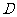分别是线段，平面图形，立体图形时，相应的＂测度＂分别是长度，面积和体积．

(3)区域为＂开区域＂；

(4)区域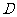内随机取点是指：该点落在区域内任何一处都是等可能的，落在任何部分的可能性大小只与该部分的测度成正比而与其形状位置无关．

[精典范例]

例1　 判断下列试验中事件A发生的概率是古典概型，还是几何概型．

(1)抛掷两颗骰子，求出现两个“4点”的概率；

(2)如图所示，图中有一个12等分的圆盘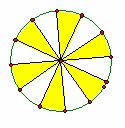，甲乙两人玩游戏，向圆盘投掷可视为质点的骰子，规定当骰子落在阴影区域时，甲获胜，否则乙获胜，求甲获胜的概率．

[分析]本题考查的几何概型与古典概型的特点，古典概型具有有限性和等可能性．而几何概型则是在试验中出现无限多个结果，且与事件的区域长度有关．

[解](1)抛掷两颗骰子，出现的可能结果有6×6=36种，且它们都是等可能的，因此属于古典概型；

(2)游戏中骰子落在阴影区域时有无限多个结果，而且不难发现“骰子落在阴影部分”，概率可以用阴影部分的面积与总面积的比来衡量，即与区域长度有关，因此属于几何概型．

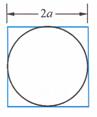例2取一个边长为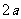的正方形及其内切圆(如右图)，随机向正方形内丢一粒豆子，求豆子落入圆内的概率．(＂测度＂为面积)

[分析]由于是随机丢豆子，故可认为豆子落入正方形内任一点的机会都是均等的，于是豆子落入圆中的概率应等于圆面积与正方形面积的比．

[解]记＂豆子落入圆内＂为事件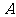，则

．

答：豆子落入圆内的概率为．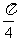

思维点拔：

2．几何概型的基本特点：

(1)试验中所有可能出现的结果(基本事件)有无限多个；

(2)每个基本事件出现的可能性相等．

1．几何概型的概念：　　　

对于一个随机试验，我们将每个基本事件理解为从某个特定的几何区域内随机地取一点，该区域中每一点被取到的机会都一样；而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点．这里的区域可以是线段，平面图形，立体图形等．用这种方法处理随机试验，称为几何概型．

3、正确判别古典概型与几何概型,会进行简单的几何概率计算．

[课堂互动]

自学评价

试验1 取一根长度为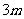的绳子，拉直后在任意位置剪断．剪得两段的长都不小于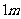的概率有多大？

试验2 射箭比赛的箭靶涂有五个彩色得分环．从外向内为白色，黑色，蓝色，红色，靶心是金色．金色靶心叫＂黄心＂．奥运会的比赛靶面直径为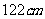，靶心直径为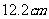．运动员在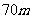外射箭．假设射箭都能射中靶面内任何一点都是等可能的．射中黄心的概率为多少？

[分析]第一个试验，从每一个位置剪断都是一个基本事件，剪断位置可以是长度为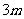的绳子上的任意一点．

第二个试验中，射中靶面上每一点都是一个基本事件，这一点可以是靶面直径为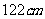的大圆内的任意一点．

在这两个问题中，基本事件有无限多个，虽然类似于古典概型的＂等可能性＂，但是显然不能用古典概型的方法求解．

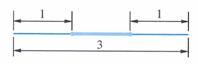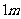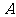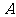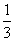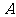[解]实验1中，如下图，记＂剪得两段的长都不小于＂为事件．把绳子三等分，于是当剪断位置处在中间一段上时，事件发生．由于中间一段的长度等于绳长的，于是事件发生的概率．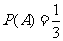

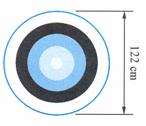　 实验2中，如下图，记＂射中黄心＂为事件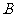，由于中靶心随机地落在面积为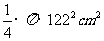的大圆内，而当中靶点落在面积为

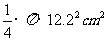的黄心内时，事件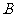发生，

于是事件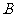发生的概率为

．

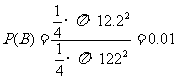[小结]

2、熟练掌握几何概型的概率公式；

1、了解几何概型的概念及基本特点；