
4.求适合不等式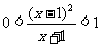 的x的整数解 (x=2)
的x的整数解 (x=2)
3.解不等式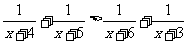
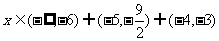
2.求不等式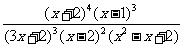 的解集
的解集
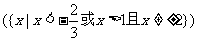
补充:
1.k为何值时,不等式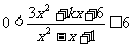 对任意实数x恒成立
对任意实数x恒成立
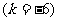
解:原不等式等价于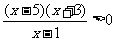
∴原不等式的解为: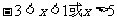
例七 k为何值时,下式恒成立: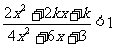
解:原不等式可化为: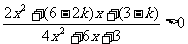
而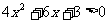
∴原不等式等价于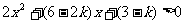
由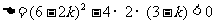 得1<k<3
得1<k<3
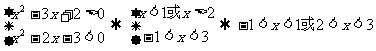
或
∴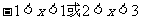
解二:(列表法)原不等式可化为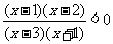 列表(见P23略)
列表(见P23略)
注意:按根的由小到大排列
解三:(标根法)作数轴;标根;画曲线,定解

小结:在某一区间内,一个式子是大于0(还是小于0)取决于这个式子的各因式在此区间内的符号;而区间的分界线就是各因式的根;上述的列表法和标根法,几乎可以使用在所有的有理分式与高次不等式,其中最值得推荐的是“标根法”
例二 解不等式 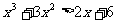
解:原不等式化为 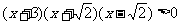
∴原不等式的解为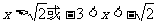
例三 解不等式 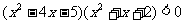
解:∵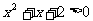 恒成立
恒成立
∴原不等式等价于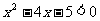 即-1<x<5
即-1<x<5
例四 解不等式 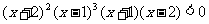
解:原不等式等价于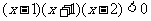 且
且 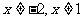
∴原不等式的解为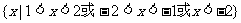
若原题目改为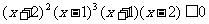 呢?
呢?
例五 解不等式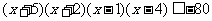
解:原不等式等价于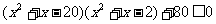
即: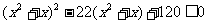
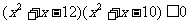
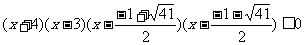
∴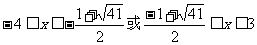
当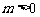 时,
时,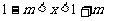 ∴
∴ 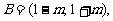
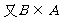 ∴
∴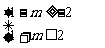 ∴
∴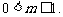
当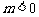 时,
时,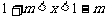 ∴
∴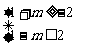 ∴ -1≤m<0.
∴ -1≤m<0.
当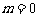 时,
时,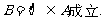
综合得: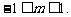
(18).⑴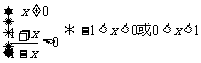 ,故f(x)的定义域为(-1,0)∪(0,1).
,故f(x)的定义域为(-1,0)∪(0,1).
⑵ ∵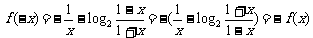 , ∴f(x)是奇函数。
, ∴f(x)是奇函数。
⑶ 设0<x1<x2<1,则
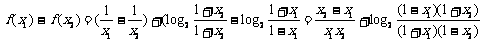
∵ 0<x1<x2<1, ∴x2-x1>0, x1x2>0,
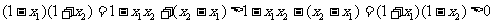
∴ 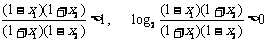 ,
,
∴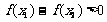 , 即
, 即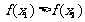 ∴
∴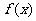 在(0,1)内递减。
在(0,1)内递减。
另解: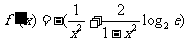 ∴当x∈(0,1)时,
∴当x∈(0,1)时,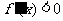
故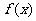 在
在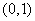 内是减函数。
内是减函数。
(19).设生产x吨产品,利润为y元,则
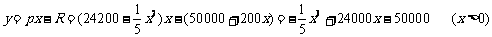

∴ 当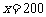 时,
时,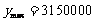 (元) 答:略。
(元) 答:略。
(20)(Ⅰ)令x-2=t,则x=t+2.
由于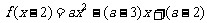 ,
,
所以 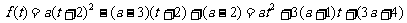
∴ 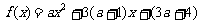
∵ 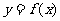 的图象关于y轴对称 ∴
的图象关于y轴对称 ∴ 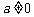 且
且 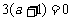 ,即
,即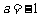
故 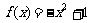
(Ⅱ)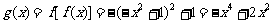
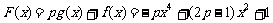
设存在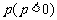 ,使F(x)满足题目要求,则当-∞<x1<x2≤-3时,F(x)是减函数,即
,使F(x)满足题目要求,则当-∞<x1<x2≤-3时,F(x)是减函数,即
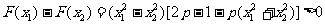
由假设-x1>-x2≥3>0, ∴ 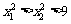
∴ 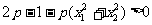 … … … … … ①
… … … … … ①
又 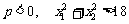 ∴
∴ 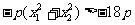
∴ 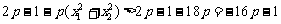
要使①式恒成立,只须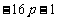 ≥0 即
≥0 即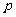 ≤
≤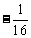
又当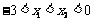 时,F(x)是增函数,
时,F(x)是增函数,
即 F(x1)-F(x2)<0,也就是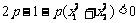 … … ②
… … ②
此时 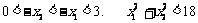
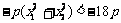 ,
, 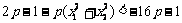
要使②式恒成立,只须 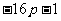 ≤0 即
≤0 即 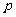 ≥
≥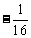
故存在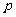 =
=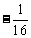 满足题目要求。
满足题目要求。
另解: 依题意F(-3)是F(x)的极小值, ∴ 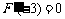 .
.
∵ 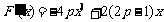 , ∴
, ∴ 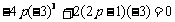 ,
,
即 . 当
. 当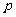 =
=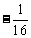 时,
时,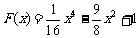 ,
, 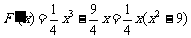
∴当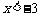 时,
时,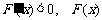 在
在 上是减函数;
上是减函数;
当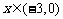 时,
时,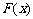 是增函数。
是增函数。
故存在 满足题目要求。
满足题目要求。
(16)①、②、③(推证f(x+2)=f(x)=f(-x))
(一) 集合与简易逻辑、函数参考答案
集合与简易逻辑、函数参考答案
1 CBACB ADDAC DC
提示:(4)A*B={2,3,4,5}(11)推证f(x+2)=f(x);(12)①、②显然正确,③不正确,④正确(∵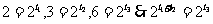 )
)
(17)(本小题满分8分)
已知集合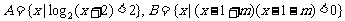 ,若
,若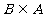 ,求实数
,求实数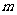 的取值范围.
的取值范围.
(18)(本小题满分10分)已知函数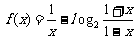 .
.
(1)求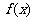 的定义域;(2)讨论
的定义域;(2)讨论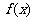 的奇偶性;(3)证明
的奇偶性;(3)证明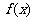 在(0,1)内单调递减.
在(0,1)内单调递减.
(19)(本小题满分10分) 某工厂生产某种产品,已知该产品的产量x(吨)与每吨产品的价格P(元/吨)之间的关系为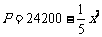 ,且生产x吨的成本为R=50000+200x元。问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
,且生产x吨的成本为R=50000+200x元。问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(20) (本小题满分12分)已知函数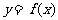 的图象关于y轴对称,且满足
的图象关于y轴对称,且满足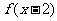
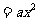
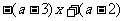 .
.
(Ⅰ)求函数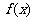 的解析式;
的解析式;
(Ⅱ)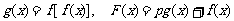 ,问是否存在
,问是否存在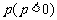 使F(x)在区间
使F(x)在区间 上是减函数,且在区间(-3,0)内是增函数?试证明你的结论。
上是减函数,且在区间(-3,0)内是增函数?试证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com