
1.安徽省两地2010届高三第一次联考检测以速度v0水平抛出一小球,如果从抛出到某时刻小球的竖直分位移与水平分位移大小相等,以下判断正确的是( C )
A.此时小球的竖直分速度大小等于水平分速度大小
B.此时小球的速度大小为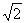 v0
v0
C.小球运动的时间为2 v0/g
D.此时小球速度的方向与位移的方向相同
6.若x, y, z
> 0,则
作ÐAOB = ÐBOC = ÐCOA = 120°, 设|OA| = x, |OB| = y, |OC| = z
5. 记
记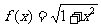 ,a > b > 0,则| f (a) - f (b) | < | a - b|
,a > b > 0,则| f (a) - f (b) | < | a - b|
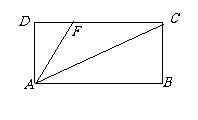
构造矩形ABCD, F在CD上,
使|AB| = a, |DF| = b, |AD| = 1,
则|AC| - |AF| < |CF|
4.若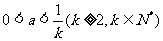 ,且a2 < a - b,则
,且a2 < a - b,则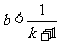
令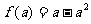 ,又
,又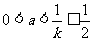 ,
,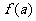 在
在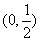 上单调递增
上单调递增
∴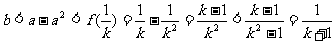
3.若x > 0, y > 0, x + y = 1,则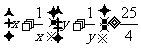
左边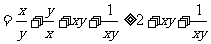 令 t = xy,则
令 t = xy,则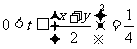
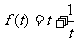 在
在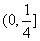 上单调递减 ∴
上单调递减 ∴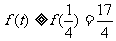
2.已知关于x的不等式(a2 - 1)x2 - (a - 1)x - 1 < 0 (aÎR),对任意实数x恒成立,求证: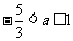 。
。
分a2 - 1 = 0和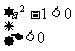 讨论
讨论
1.
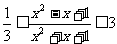
令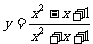 ,则 (y - 1)x2 + (y + 1)x + (y
- 1) = 0
,则 (y - 1)x2 + (y + 1)x + (y
- 1) = 0
用△法,分情况讨论
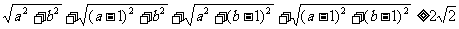
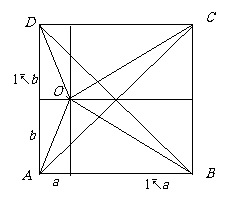 证:构造单位正方形,O是正方形内一点
证:构造单位正方形,O是正方形内一点
O到AD, AB的距离为a, b,
则|AO| + |BO| + |CO| + |DO|≥|AC| + |BD|
其中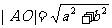 ,
,
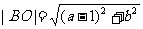
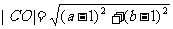
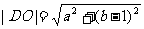 又:
又: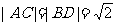
∴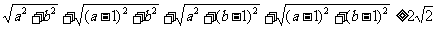
证:设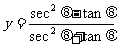 则:(y - 1)tan2q + (y + 1)tanq + (y - 1) = 0
则:(y - 1)tan2q + (y + 1)tanq + (y - 1) = 0
当 y = 1时,命题显然成立
当 y ¹ 1时,△= (y + 1)2 - 4(y - 1)2 = (3y - 1)(y - 3)≥0
∴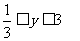
综上所述,原式成立。(此法也称判别式法)
3.构造图形法:
证:由题设:显然a, b, c中必有一个正数,不妨设a > 0,
则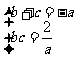 即b, c是二次方程
即b, c是二次方程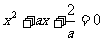 的两个实根。
的两个实根。
∴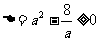 即:a≥2
即:a≥2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com