
3. 如图,已知矩形OABC的长OA= ,宽OC=1,将△AOC沿AC翻折得△APC.
,宽OC=1,将△AOC沿AC翻折得△APC.
(1)填空:∠PCB= 度,P点坐标为 ;
(2)若P、A两点在抛物线y=-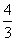 x2+bx+c上,求b、c的值,并说明点C在此抛物线上;
x2+bx+c上,求b、c的值,并说明点C在此抛物线上;
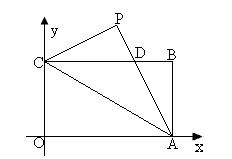 ﹡(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由.
﹡(3)在(2)中的抛物线CP段(不包括C,P点)上,是否存在一点M,使得四边形MCAP的面积最大?若存在,求出这个最大值及此时M点的坐标;若不存在,请说明理由.
2. (06沈阳) 某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,则所获利润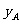 (万元)与投资金额
(万元)与投资金额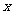 (万元)之间存在正比例函数关系:
(万元)之间存在正比例函数关系: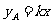 ,并且当投资5万元时,可获利润2万元;
,并且当投资5万元时,可获利润2万元;
信息二:如果单独投资B种产品,则所获利润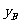 (万元)与投资金额
(万元)与投资金额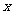 (万元)之间存在二次函数关系:
(万元)之间存在二次函数关系: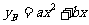 ,并且当投资2万元时,可获利润2.4万元;当投资4万元,可获利润3.2万元.
,并且当投资2万元时,可获利润2.4万元;当投资4万元,可获利润3.2万元.
(1) 请分别求出上述的正比例函数表达式与二次函数表达式;
(2) 如果企业同时对A、B两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少.
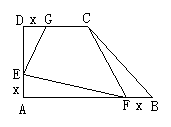
1. 如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4;求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
2. 每件商品的利润P = - ;商品的总利润Q = × .
[典例精析]
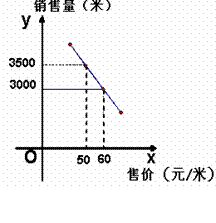
例1 近年来,“宝胜”集团根据市场变化情况,采用灵活多样的营销策略,产值、利税逐年大幅度增长.第六销售公司2004年销售某型号电缆线达数万米,这得益于他们较好地把握了电缆售价与销售数量之间的关系.经市场调研,他们发现:这种电缆线一天的销量y(米)与售价x(元/米)之间存在着如图所示的一次函数关系,且40≤x≤70.
(1) 根据图象,求y与x之间的函数解析式;
(2) 设该销售公司一天销售这种型号电缆线的收入为w元.
① 试用含x的代数式表示w;
② 试问当售价定为每米多少元时,该销售公司一天销售该型号电缆的收入最高?最高是多少元?
例2
(08南宁)随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润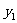 与投资量
与投资量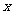 成正比例关系,如图(1)所示;种植花卉的利润
成正比例关系,如图(1)所示;种植花卉的利润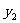 与投资量
与投资量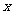 成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
成二次函数关系,如图(2)所示(注:利润与投资量的单位:万元)
⑴ 分别求出利润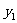 与
与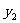 关于投资量
关于投资量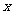 的函数关系式;
的函数关系式;
⑵ 如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?
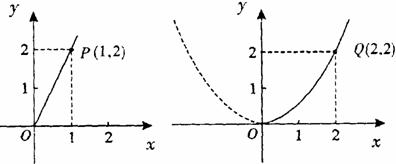
(1) (2)
[中考演练]
1.二次函数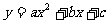 通过配方可得
通过配方可得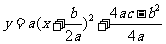 ,
,
⑴ 当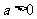 时,抛物线开口向 ,有最 (填“高”或“低”)点, 当
时,抛物线开口向 ,有最 (填“高”或“低”)点, 当
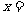 时,
时,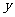 有最 (“大”或“小”)值是
;
有最 (“大”或“小”)值是
;
⑵ 当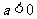 时,抛物线开口向 ,有最 (填“高”或“低”)点, 当
时,抛物线开口向 ,有最 (填“高”或“低”)点, 当
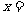 时,
时,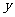 有最 (“大”或“小”)值是 .
有最 (“大”或“小”)值是 .
3.(06贵阳) 某商场购进一种单价为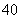 元的篮球,如果以单价
元的篮球,如果以单价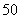 元售出,那么每月可售出
元售出,那么每月可售出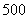 个.根据销售经验,售价每提高
个.根据销售经验,售价每提高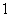 元,销售量相应减少
元,销售量相应减少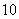 个.
个.
⑴ 假设销售单价提高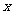 元,那么销售每个篮球所获得的利润是___________元;这种篮球每月的销售量是___________个.(用含
元,那么销售每个篮球所获得的利润是___________元;这种篮球每月的销售量是___________个.(用含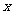 的代数式表示)
的代数式表示)
⑵ 当篮球的售价应定为 元时,每月销售这种篮球的最大利润,此时最大利润是 元.
[考点链接]
2.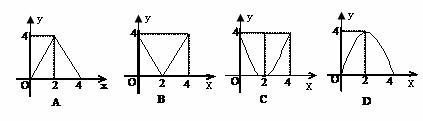 如图,已知
如图,已知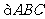 中,BC=8,BC上的高
中,BC=8,BC上的高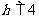 ,D为BC上一点,
,D为BC上一点,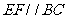 ,交AB于点E,交AC于点F(EF不过A、B),设E到BC的距离为
,交AB于点E,交AC于点F(EF不过A、B),设E到BC的距离为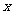 ,则
,则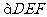 的面积
的面积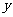 关于
关于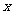 的函数的图像大致为( )
的函数的图像大致为( )
1.(08甘肃)如图是某种蜡烛在燃烧过程中高度与
时间之间关系的图像,由图像解答下列问题:
⑴ 此蜡烛燃烧1小时后,高度为 cm;
经过 小时燃烧完毕;
⑵ 这个蜡烛在燃烧过程中高度与时间之间关系
的解析式是 .
22.(本小题满分14分)
已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(III)求证直线MA、MB与x轴始终围成一个等腰三角形.
21. (本小题满分12分)
已知定义在R上的函数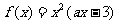 ,其中a为常数.
,其中a为常数.
(I)若x=1是函数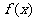 的一个极值点,求a的值;
的一个极值点,求a的值;
(II)若函数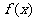 在区间(-1,0)上是增函数,求a的取值范围;
在区间(-1,0)上是增函数,求a的取值范围;
(III)若函数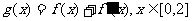 ,在x=0处取得最大值,
,在x=0处取得最大值,
求正数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com