
20.(本小题满分12分)
某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作. 已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是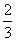 ,且每题正确完成与否互不影响. 求:
,且每题正确完成与否互不影响. 求:
(Ⅰ) 分别写出甲、乙两考生正确完成题数的概率分布列;
(Ⅱ) 试用统计知识(期望、方差)分析比较两考生的实验操作能力.
19.(本小题满分12分)
在平面直角坐标系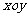 中,直线l与抛物线
中,直线l与抛物线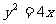 相交于不同的
相交于不同的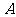 、
、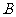 两点.
两点.
(Ⅰ)如果直线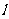 过抛物线的焦点,求
过抛物线的焦点,求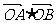 的值;
的值;
(Ⅱ)如果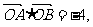 证明直线
证明直线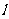 必过一定点,并求出该定点.
必过一定点,并求出该定点.
18. (本小题满分12分)
(本小题满分12分)
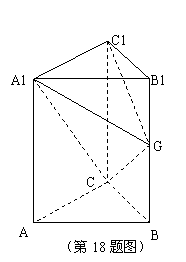
如图,在直棱柱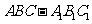 中,
中,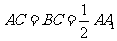 ,
,
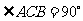 ,
,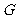 为
为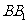 的中点.
的中点.
(Ⅰ) 求证:平面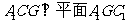 ;
;
(Ⅱ)求平面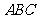 与平面
与平面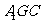 所成锐二面角的余弦值.
所成锐二面角的余弦值.
17.(本小题满分12分)
已知命题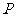 :“函数
:“函数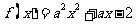 在
在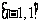 上存在零点”;
上存在零点”;
命题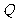 :“只有一个实数
:“只有一个实数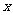 满足不等式
满足不等式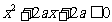 ”;
”;
若命题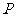 或
或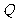 是假命题,求实数
是假命题,求实数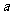 的取值范围.
的取值范围.
16. 给出下列四个命题:
①命题“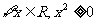 ”的否定是“
”的否定是“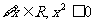 ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③抛物线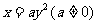 的焦点为
的焦点为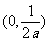 ;
;
④函数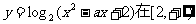 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是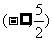 .
.
其中真命题的序号是 .(填上所有真命题的序号)
解答题:本大题共6个小题,共74分.
15.定义运算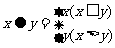 ,若
,若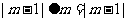 ,则
,则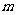 的取值范围是
.
的取值范围是
.
14.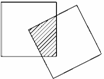 现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是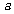 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为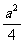 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为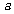 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为
.
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为
.
13. 设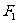 和
和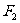 为双曲线
为双曲线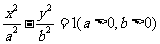 的两个焦点,
若
的两个焦点,
若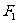 、
、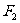 、
、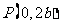 是正三角形的三个顶点,则双曲线的离心率为 .
是正三角形的三个顶点,则双曲线的离心率为 .
12.设椭圆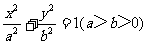 的离心率为
的离心率为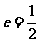 ,右焦点为
,右焦点为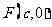 ,方程
,方程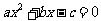 的两个实根分别为
的两个实根分别为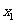 和
和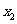 ,则点
,则点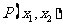
A.必在圆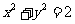 内
B.必在圆
内
B.必在圆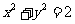 上
上
C.必在圆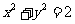 外
D.以上三种情形都有可能
外
D.以上三种情形都有可能
第Ⅱ卷(共90分)
11. 函数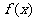 在定义域R内可导,若
在定义域R内可导,若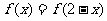 ,且当
,且当 时,
时,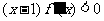 ,设
,设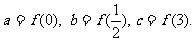 则
则
A.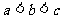 B.
B.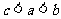 C.
C.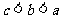 D.
D.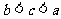
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com