2． 已知a, b, m都是正数，并且a < b，求证：

　 证：

∵a,b,m都是正数，并且a<b，∴b + m > 0 ,　 b - a > 0

∴　　 即：

　　　　 变式：若a > b，结果会怎样？若没有“a < b”这个条件，应如何判断？

1． 求证：x² + 3 > 3x

　　 证：∵(x² + 3) - 3x =

　　　　 ∴x² + 3 > 3x

2．比较法之一(作差法)步骤：作差--变形--判断--结论

1．不等式的一个等价命题

2. 已知中心在原点的双曲线C的右焦点为(2,0)，右顶点为。

(1) 求双曲线C的方程；

(2) 若直线l：与双曲线C恒有两个不同的交点A和B，且(其中O为原点)，求k的取值范围。

教学反思：

由于向量既能体现“形”的直观位置特征，又具有“数”的良好运算性质，是数形结合与转换的桥梁和纽带。而解析几何也具有数形结合与转换的特征，所以在向量与解析几何知识的交汇处设计试题，已逐渐成为高考命题的一个新的亮点。本节问题立足基础，适当综合，巧设问题，分类解析，有条理有内容有方法有深度，正确理解和发动学生多看、多想、多操作、多反思总结，突出学生主体地位，较好的完成教学目标。

附板书设计：

3．⑴　 ⑵ k的取值范围是(－1,1)。

从上述几例可以看出，只要对于解析几何中图形的位置关系和数量关系进行认真分析，充分挖掘问题的向量背景，注意运用曲线参数方程的点化作用，就完全有可能获得一个漂亮的向量解法。

课时小结

向量具有数形兼备的特点，成为了作为联系众多知识的桥梁，向量与三角、解析几何、立体几何的交汇是当今高考命题的必然趋势,本节处理了三类问题，即利用向量解决解析几何中有关平行、共线问题，长度、角度、垂直及轨迹和综合应用问题。

布置作业：

1已知椭圆方程，过B(－1，0)的直线l交随圆于C、D两点，交直线x＝－4于E点，B、E分的比分λ₁、λ₂．

求证：λ₁+λ₂＝0

3．已知点G是△ABC的重心，A(0, －1)，B(0, 1)，在x轴上有一点M，满足||=||， (∈R)．

⑴求点C的轨迹方程；

⑵若斜率为k的直线l与点C的轨迹交于不同两点P，Q，且满足||=||，试求k的取值范围．

答案1．B　 2．　

2、已知，椭圆的两个焦点，P()为椭圆上一点，

当<0时，的取值范围为＿＿＿＿＿＿＿＿＿.。

1、平面直角坐标系中，为坐标原点，已知，若点满足，其中，且，则点的轨迹方程为(　 )

A. 　　B.

C. 　　　　D.

3、运用平面向量综合知识，探求动点轨迹方程，还可再进一步探求曲线的性质。

例2．已知是x,y轴正方向的单位向量，设=, =,且满足||+||=4.

⑴求点P(x,y)的轨迹C的方程.

⑵如果过点Q(0，m)且方向向量为 =(1,1) 的直线l与点P的轨迹交于A，B两点，当AOB的面积取到最大值时，求m的值。

解：(1) =, ||=,且||+||=4.

点P(x,y)到点(,0)，(-,0)的距离这和为4，故点P的轨迹方程为

(2)设A(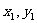),B()依题意直线AB的方程为y=x+m.代入椭圆方程，得，则+=-m, =

因此，

当时，即m=时，

[变式1] 已知是x,y轴正方向的单位向量，设=, =,且满足|||-|||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)

[变式2] 已知是x,y轴正方向的单位向量，设=, =,且满足=||.求点P(x,y)的轨迹C的方程.

[提示：设K(-,0)，F (,0)，则表示在x轴上射影，即点P到x= -的距离，所以点P到定点F的距离与到定直线x= -的距离比为1，故点P的轨迹是以(,0)为焦点以x= -为准线抛物线]

巩固训练