
4.集合问题多与函数、方程有关,要注意
各类知识的融会贯通.
[精典范例]
例1. 设U={1,2,3,4,5},且A∩B={2},
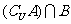 ={4},
={4},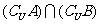
={1,5},则下列结论正确的是
( )
A.3∈A,3∈B
B.2∈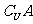 ,3∈B
,3∈B
 C.3∈
C.3∈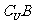 ,3∈A
,3∈A
D.3∈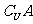 ,3∈
,3∈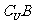
分析:按题意画出Venn图即可找出选择
的分支.
[解]
画出满题意足Venn图:
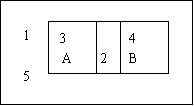
由图可知:3∈A且3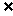 B,即3∈A且
B,即3∈A且
3∈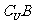 , ∴ 选C.
, ∴ 选C.
点评:
本题可用排除法来解,若选A,则3∈
A∩B,与已知A∩B={2}矛盾,……显然这种方法没有Venn图形象直观,这也突出数形集结合的思想在集合中的运用.
追踪训练一
3.含参数的集合问题,多根据集合的的互异性处理,有时需要用到分类讨论、数形集结合的思想.
2.关于集合中的运算,一般应把各参与运算的集合化到最简形式,然后再进行运算.
1.对于集合的问题:要确定属于哪一类集合(数集,点集,或某类图形集),然后再确定处理此类问题的方法.
4.再解决有关集合问题时,要注意各种思想方法(数形集结合、补集思想、分类讨论)的运用.
[课堂互动]
自学评价
3.掌握集合的运算(交、并、补);
2.掌握集合的包含关系(子集、真子集);
1.掌握集合的有关基本义概念,运用集合的概念解决问题;
5、设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0,a∈R}.
(1)若A∩B=B,求实数a的值。
(2)若A∪B=B,求实数a的值。
4、集合{3,x,x2-2x}中,x应满足的条件是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com