5．当x∈［－2，2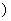时，y=3^－x－1的值域是　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A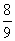．［－，8］　　　　 B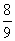．［－，8］　　　　 C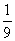．(，9)　　　　　　　 D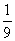．［，9］

4．设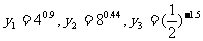，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．y₃＞y₁＞y₂　　　　　 B．y₂＞y₁＞y₃　　　　　 C．y₁＞y₂＞y₃　　　　　 D．y₁＞y₃＞y₂

3．设函数　　　　　　　　　　　　　 (　　 )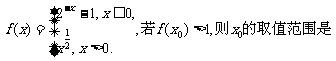

　　　 A．(－1，1)　　　　　　　　　　　　　　　　　　　　　　 B．(－1，+)

　　　 C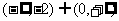．　　　　　　　　　　　　　　 D．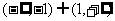

2．化简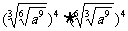的结果为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．a¹⁶ B．a⁸ C．a⁴ D．a²

1．化简［3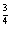］的结果为　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

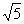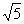A．5　　　　　　　　　　　　 B．　　　　　　　　　　 C．－　　　　　　　　 D．－5

26．解：(1)过D₁作D₁E⊥x轴于E，

　　　　 ∵∠DA D₁=30°，AD∥D₁ E，　　　　

　　　　 ∴∠A D₁E=30°，

　　　　 又n=，

　　　　 ∴A D₁=2，即正方形ABCD的边长为2

　 (2)∵∠DA D₁=30°，

　　　　 ∴∠B₁AO=30°=.∠DA D₁=30°，

　　　　 ∴直线D₁ C₁的解析式为y=－tan30°x,

　　　　 即y=－x.

　 (3)如图，过C₁作直线GF∥y轴，交D₁F于F，其中D₁F∥x轴.

　　　　 ∵A D₁=D₁ C₁,

　　　　　 ∠D₁EA=.∠D₁F C₁=90°

　　　　　 ∠D₁AE=.∠D₁C₁ F

　　　 　∴△D₁AE≌△D₁C₁ F

　　　　 ∴D₁E= D₁ F

　　　　 又m+n=－2,

　　　　 ∴G(－2,0)

　　　　 而O C₁=，

　　　　 ∴G C₁=1~①

　　　　 由△OC₁G∽△OD₁ E

　　　　 得＝，即＝, C₁G=~②

　　　　 联立①、②得：=－,直线D₁ C₁的解析式为y=－x.

25．(1)证明：∵AB为圆O₁之直径

　　　　　　 ∴∠ADB=90°，

　　　　　　 又∠ADB与∠ADC互补

　　　　　　 ∴∠ADC=90°，

　　　　　　 ∴AC是⊙O₂的直径;

　　 (2)证明：连结O₁O₂，

　　　　　　 ∵=且∠BAC=∠O₁A O₂

　　　　　　 ∴△AO₁O₂∽△ABC

　 　　　　　　又O₁A= O₁O₂

　　　　　　 ∴AB=BC

　　 (3)解：设AG=x

　　　　　 ∵A O₂= O₂C且AB=BC

　　　　　 ∴AB=BC=4

　　　　　 而∠DAC=∠O₂BC，∠A O₂B=∠B O₂C，

　　　　　 ∴△AGO₂∽△BCO₂

　　　　　 　∴= ，解得：x=

24．解：(1)当m=1时，

　　　　　　 原方程为x²－2x－1=0,解得

　　　　　　 　x=1±

　　　　 (2)△=8m

　　　　　　 ①当m>0时，原方程有两不等实根；

　　　　　　 ②当m=0时，原方程有两相等实根；

　　　　　　 ③当m<0时，原方程无实根.

　　　 　(3)由已知，可得：0<x₂－x₁<3

　　　　　　 两边平方可得到：

　　　　　　 (x₁+ x₂)²－4 x₁x₂<9

　　　　　　 即8m<9，解得m<

　　　　　　 而x₁≠ x₂且m为整数

　　　　　　 ∴m=1

23．证明：(1)∵BE平分∠ABC

　　　　　　　 ∴∠ABE=∠CBE，

　　　　　　　 又△ABD∽△EBC

　　 　　　　　∴=即BD·BE=AB·BC

　　　　 (2)∵∠ADB=∠EDC，

　　　　　　 又∠BAC=∠ECB=90°，

　　　　　　 ∴∠ABE=∠CBE=∠ACE

　　　　　　 而AB=AC

　　　　　　 ∴△ADB≌△AFC

　　　　　　 ∴CF=BD

22．解：(1)解法一：在△ABC与△DEF中，若∠A=∠D，AC=DF，AB=DE，则△ABC≌△DEF.

　　　 解法二：在△ABC与△DEF中，若AC=DF，AB=DE，△ABC的周长与△DEF的周长相等，则△ABC≌△DEF.

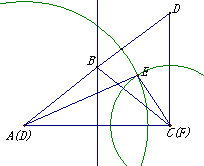　 (2)解法一：假命题：在△ABC与△DEF中，若△ABC的周长与△DEF的周长相等且AC=DF，则△ABC≌△DEF.

　　　　　　　 反例：如图，作直线AC=DF，取AC之中垂线l，在l上任取一点B，连结AB、BC，延长AB与CD交于点D，其中CD⊥AC，以A为圆心，r为半径画弧(0<r<AD且r≠AB),再以C为圆心，AD－r为半径画画弧，两弧交于一点E，显然，此时△ABC与△DEF并不全等.

　　　 解法二：假命题：在△ABC与△DEF中，若△ABC的周长与△DEF的周长相等且AB=DE，则△ABC≌△DEF.

　　　　　　　 反例：作法形如法一.

　　　 解法三：假命题：在△ABC与△DEF中，若△ABC的周长与△DEF的周长相等且∠A=∠D，则△ABC≌△DEF.

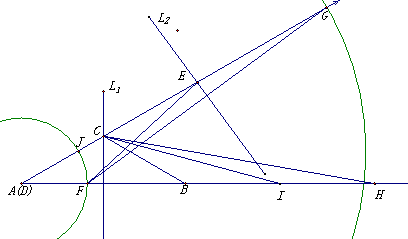　　　　　　　 反例：如图，作∠A=∠D，取定长AB，作AB之中垂线L₁，交角A的另一边于C,，连接BC则作出△ABC，在AB边上取BI=BC，IH=BC，以J为圆心，FH为半径画弧交AB于G，连结FG，作FG之中垂线L₂，交AC于E，连接EF，则作出了△DEF，显然，此时△ABC与△DEF并不全等.