
3.通过解综合题提高学生解综合题的能力.
教学重点和难点
教学的重点是进一步掌握三垂线定理及其逆定理,并能灵活的应用它们来解有关的题.教学的难点是在空间图形中有许多平面时,如何选好“基准平面”和“第一垂线”.
教学设计过程
师:上一节我们应用三垂线定理及其逆定理讲了四个例题.其中大多是基本题.今天我们一方面要在应用这些基本题的基础上解有关的综合题;另外我们再来解其它的综合题来提高我们的解综合题的能力.现在看例1.
例1 如图1,已知:PA⊥PB,PA⊥PC,PB⊥PC,求证:
△ABC是锐角三角形.
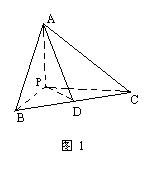
师:这一题证法很多,所以我们要多想几种证法.
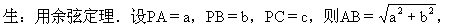
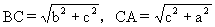
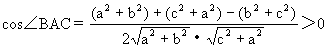
所以 ∠BAC是锐角.
同理可证∠ABC,∠ACB都是锐角.
师:我们能不能直接用三垂线定理来证?
生:由已知可得PA⊥平面PBC.在直角三角形PBC中,作PD⊥BC于D,因为∠PBC,∠PCB都是锐角,所以垂足D一定在斜边BC内部,连PD,则PD⊥BC(三垂线定理).对于△ABC来说,因垂足D在BC边内部,所以∠ABC,∠ACB都是锐角,同理可证∠BAC也是锐角.
师:能不能用公式cosθ1·cosθ2=cosθ来证明△ABC为锐角三角形?
生:因AP⊥平面PBC,所以∠ABP是线面角,相当于θ1,∠PBC相当于θ2,因θ1,θ2都是锐角.所以cosθ1>0,cosθ2>0,cosθ=cosθ1·cosθ2>0,所以θ为锐角。即∠ABC是锐角,同理可证∠BAC,∠ACB都是锐角.
师:我们用了三种方法来证明△ABC是锐角三角形,现在我们换一个角度来研究这个基本图形另外一个性质.看例2.
例2 如图2,已知:PA⊥PB,PA⊥PC,PB⊥PC.PH⊥平面ABC于H.求证:H点是△ABC的垂心.
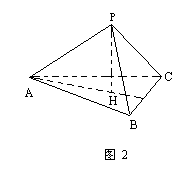
师:垂心是三角形三边垂线(高线)的交点,要证H是△ABC的垂心,只要证AH⊥BC即可.
生:因为 PA⊥BP,
PA⊥CP,
所以 PA⊥平面PBC.
故 PA⊥BC.
对于平面ABC来说,PH是垂线,
PA是斜线,AH是PA在平面ABC内的射线.
因为 PA⊥BC,所以 AH⊥BC.
同理可证BH⊥AC,CH⊥AB.
故H是△ABC的垂心.
师:由例2的演变可得例3,现在我们来看例3.
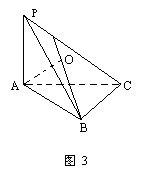
例3 如图3,△ABC中,∠BAC是锐角,PA⊥平面ABC于A,AO⊥平面PBC于O.求证:O不可能是△PBC的垂心.
师:要证明O不可能是△PBC的垂心,用什么方法?
生:用反证法.
师:为什么想到用反证法?
生:因为直接证不好证.
师:对,因为直接来证不好利用条件,而用反证法,假设O是△PBC的垂心,则这样证明的思路就“活了”,就可利用已知条件,现在我们用反证法来证明.
生:假设O是△PBC的垂心,则BO⊥PC.
对平面PBC来说,AO是垂线,AB是斜线,BO是AB在平面PBC内的射影.
因为 BO⊥PC,所以 AB⊥PC.
又因为 PA⊥平面ABC,PA⊥AB,
所以AB⊥平面PAC,AB⊥AC,∠BAC是直角,与已知∠BAC是锐角相矛盾.所以假设不能成立,所以O不可能是△PBC的垂心.
师:分析例3我们可以看出例3是由例2演变而来.也就是说在PA⊥AB,PA⊥ACO是△PBC的垂心条件下一定可以推导出AB⊥AC.是例2的逆命题再加以演变而得.现在我们来看例4.
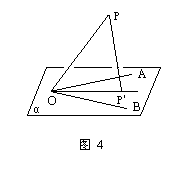
例4 如图4,已知:∠AOB在平面α内,∠AOB=60°,PO是平面α的一条斜线段,∠POA=∠POB=45°,PP′⊥平面α于P′,且PP′=3.求:
(1)PO与平面α所成的角的正弦;
(2)PO的长.
师:我们如何利用上节课所讲的两个基本题来解这题.
生:因∠POA=∠POB,所以OP′是∠AOB的平分线,∠POP′相当于θ1,θ2=30°,θ=45°,由cosθ1·cos30°=cos
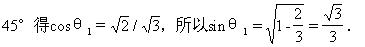
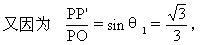
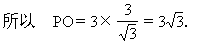
师:在我们脑中如果“储存”许多基本题,那么在我们解有关综合题时,就能“得心应手”.所以在平时我们一定要注意对基本题的理解、掌握,解这题的思路就是一个典型.下面我们来看例5.
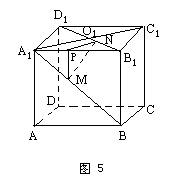
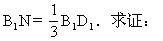
(1)直线MN是异面直线A1B和B1D1的公垂线;
(2)若这个正方体的棱长为a,求异面直线A1B和B1D1的距离.
师:我们是在讲三垂线定理及其逆定理应用时讲这个例题的.所以我们想法用三垂线定理或它的逆定理来证明这一题.要用三垂线定理首先要确定对于哪一个平面来用三垂线定理.
生:对于平面A1B1C1D1来用三垂线定理.
师:这时MN是平面A1B1C1D1的斜线,我们如何作平面A1B1C1D1的垂线呢?
生:作MP⊥A1B1于P,又因为D1A1⊥平面A1ABB1,所以A1D1⊥PM,故PM⊥平面A1B1C1D1.
师:对于平面A1B1C1D1来说,MP是垂线,MN是斜线,NP是MN在平面A1B1C1D1上的射影.我们要证MN⊥B1D1,只要证PN⊥B1D1即可.在正方形A1B1C1D1中,我们知道A1C1⊥B1D1,所以现在只要证PN∥A1Q1即可.我们如何利用已知条件来证PN∥A1O1.
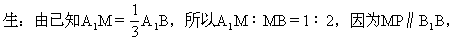
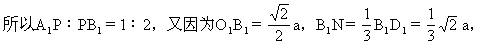
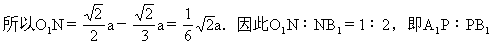
=O1N∶NB1,所以PN∥A1O1,所以PN⊥B1D1,故MN⊥B1D1.同理可证MN⊥A1B,所以MN是异面直线A1B和B1D1的公垂线.
师:已知正方体的棱长为a,在直角三角形MNP中,如何求出MN的长?

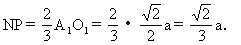
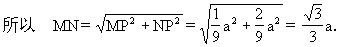
师:这是一道很好、很典型的题,它很巧妙、很直接地求出异面直线A1B,B1D1的公垂线及这两异面直线的距离.这一道题我们的先人们是如何想出来的?这一问题我们利用课外活动时间来进行探索.
今天就讲这五个例题,讲这五个例题的目的一是进一步应用三垂线定理及其逆定理,二是应用上节课刚讲过的基本题来解较综合的题.
作业
补充题
2.应用上一节课上所讲的两个基本题来解有关的综合题;
1.进一步理解、巩固并应用三垂线定理及其逆定理;
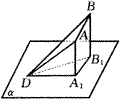
19.如图,α表示地面,第一次观测时气球在A点,第二次观测时气球在B点,A、B两点在地面的投影点分别是A1、B1,依题意:AA1=14×10=140(m),
BB1=14×20=280(m),
∠A1DB1=30°,∠ADA1=45°,∠BDB1=60°.
∴ A1D=AA1=140(m),
B1D=BB1ctg60°=(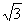 /3)×280(m).
∴ 在△A1B1D中,
A1B1=
/3)×280(m).
∴ 在△A1B1D中,
A1B1=
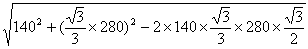 =(140 =(140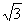 /3). /3). |
又 B1D2=(1/3)×2802,
A1D2+A1B12=1402+(1402/3)=(2802/3)=B1D2,
故∠B1A1D=90°.
综上,风向为正南,风速为(140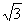 /3)/10=(14
/3)/10=(14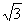 /3)(m/分).
20.见2000年高考理科第18题.(略)
/3)(m/分).
20.见2000年高考理科第18题.(略)
18.见1999年高考题,从略.
 |
|
第19题 |
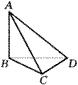
9.(1)如图甲,连结BD、AC、AD.
|
AB⊥BC |
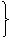 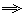 |
AB⊥平面BCD |
|
|
AB⊥CD |
|
|
|
平面ABD经过AB |
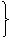 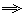 平面ABD⊥平面BCD,平面ABC⊥平面BCD. 平面ABD⊥平面BCD,平面ABC⊥平面BCD. |
|
|
|
平面ABC经过AB |
根据三垂线定理,得CD⊥AC.又CD⊥BC,∴CD⊥平面ABC,∴平面ABC⊥平面ACD.因此有三个直二面角A-BD-C,A-BC-D,D-AC-B.
 |
|
第9题(甲) |
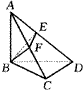
对于(2),首先应找出对应角,再考虑范围或余弦值. (2)AB⊥平面BCD,∴AD与平面BCD所成的角∠ADB=α,CD⊥平面ABC,AD与平面ABC所成的角∠DAC=β. 由最小角定理(斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角)知α<∠ADC,所以 0°<α+β<∠ADC+β=90°.? 过B作BE⊥AD,垂足为E,过B作BF⊥AC,垂足为F(参见图乙),可证CD⊥BF,AC⊥BF,?∴BF⊥平面ACD.又BE⊥AD,?根据三垂线定理可得AD⊥EF,
 |
|
第9题(乙) |
∴∠BEF是二面角B-AD-C的平面角.
?cos∠BEF=(EF/BE)
=(AEtgβ)/[AEtg(90°-α)]=tgαtgβ.
对于第(3)问,得首先建立目标函数,再求最大值.
(3)AD=a,AB=Asinα,BD=Acosα,CD=Asinβ.
V=(1/3)S△BCD·AB=(1/3)·(1/2)BC·CD·AB
=(1/6)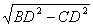 ·CD·AB
=(a3/6)·sinβsinα·
·CD·AB
=(a3/6)·sinβsinα·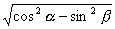 .
V2=(a6/36)(cos2α-sin2β)sin2βsin2α
≤(a6/36)·{[(cos2α-sin2β)+sin2β+sin2α]/3}3
=(a6/36)·(1/27)·(18
.
V2=(a6/36)(cos2α-sin2β)sin2βsin2α
≤(a6/36)·{[(cos2α-sin2β)+sin2β+sin2α]/3}3
=(a6/36)·(1/27)·(18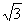 /a3).
∴Vmax2=(
/a3).
∴Vmax2=(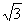 /54)a3.
此时sin2α=sin2β=cos2α-sin2β,即
2sin2α=cos2α,∴tg2α=(1/2),即tgα=(
/54)a3.
此时sin2α=sin2β=cos2α-sin2β,即
2sin2α=cos2α,∴tg2α=(1/2),即tgα=(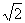 /2),此时α=β=arctg(
/2),此时α=β=arctg(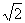 /2).
10.(1)因截面A1ECF的四边相等,且都为(
/2).
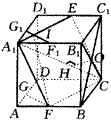
10.(1)因截面A1ECF的四边相等,且都为(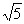 /2)a,故截面是菱形.
/2)a,故截面是菱形.
 |
|
第10题 |
又∵ ∠B1A1E=∠B1A1F,
∴ A1B1在截面内的射影是∠EA1F的平分线A1C.
故∠B1A1C即为A1B1与截面所成的角.
连结B1C,则A1B1⊥B1C,
∴ tg∠B1A1C=(B1C1/A1B1)=(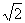 a/a)=
a/a)=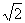 ,
∴ ∠B1A1C=arctg
,
∴ ∠B1A1C=arctg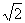 .
(2)连结BC1,则BC1∥EF,故BC1的中点O到截面A1ECF的距离即为点B到截面A1ECF的距离.
∵ 面A1B1C⊥面A1ECF,在面A1B1C内过O作OH⊥A1C,垂足为H,则OH⊥平面A1ECF,∴ OH的长为所求点B到截面A1ECF的距离.
∵ Rt△OHC∽Rt△A1B1C,
∴ (OH/A1B1)=(OC/A1C),
即OH=(A1B1·OC/A1C)=(a·(
.
(2)连结BC1,则BC1∥EF,故BC1的中点O到截面A1ECF的距离即为点B到截面A1ECF的距离.
∵ 面A1B1C⊥面A1ECF,在面A1B1C内过O作OH⊥A1C,垂足为H,则OH⊥平面A1ECF,∴ OH的长为所求点B到截面A1ECF的距离.
∵ Rt△OHC∽Rt△A1B1C,
∴ (OH/A1B1)=(OC/A1C),
即OH=(A1B1·OC/A1C)=(a·(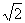 /2)a/
/2)a/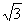 a)=(
a)=(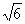 /6)a.
(3)取AG=(1/4)AD,连结GF,
∵ (AG/AF)=(FB/BC)=(1/2),
∴ Rt△GAF∽Rt△FBC.
∴ ∠GFA=∠FCB.从而∠GFA与∠CFB互余.
∴ ∠GFC=90°,即GF⊥FC.
设A1G1=(1/4)A1D1,A1F1=(1/2)A1B1,连结G1F1交A1E于I.
∵ A1E∥FC,G1F1∥GF,
∴ G1F1⊥A1E,连结FI,F1I为FI在底面A1B1C1D1上的射影.故∠FIF1为所求二面角的平面角,记为θ.
G1F1=(
/6)a.
(3)取AG=(1/4)AD,连结GF,
∵ (AG/AF)=(FB/BC)=(1/2),
∴ Rt△GAF∽Rt△FBC.
∴ ∠GFA=∠FCB.从而∠GFA与∠CFB互余.
∴ ∠GFC=90°,即GF⊥FC.
设A1G1=(1/4)A1D1,A1F1=(1/2)A1B1,连结G1F1交A1E于I.
∵ A1E∥FC,G1F1∥GF,
∴ G1F1⊥A1E,连结FI,F1I为FI在底面A1B1C1D1上的射影.故∠FIF1为所求二面角的平面角,记为θ.
G1F1=(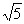 /4)a,F1I=(F1A12/GF1)=(
/4)a,F1I=(F1A12/GF1)=(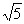 /5)a,
∴ tgθ=
/5)a,
∴ tgθ=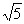 .
即所求二面角的大小为θ=arctg
.
即所求二面角的大小为θ=arctg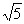 .
?§?5 立体几何的综合问题
1.B;2.D;3.B;4.D;?5.(3aV)/(2S1S2);6.576πcm2;7.45°.
8.由于煤质相同,则同样体积的两种蜂窝煤有同样的热量.
设大蜂窝煤的半径为R,高为H;小蜂窝煤的半径为r,高为h.则R=2r,H=(4/3)h.
一块大蜂窝煤的体积为πR2H,用V大表示;一块小蜂窝煤的体积为πr2h,用V小表示.所以
V大=πR2H=π(2r)2·(4/3)h
=(16/3)·πr2h=(16/3)V小,
即V大∶V小=16∶3.
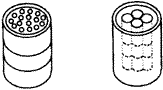
由上述数据,我们可以作出多种设计,如图所示,就是较为简单的两种炉膛设计.
.
?§?5 立体几何的综合问题
1.B;2.D;3.B;4.D;?5.(3aV)/(2S1S2);6.576πcm2;7.45°.
8.由于煤质相同,则同样体积的两种蜂窝煤有同样的热量.
设大蜂窝煤的半径为R,高为H;小蜂窝煤的半径为r,高为h.则R=2r,H=(4/3)h.
一块大蜂窝煤的体积为πR2H,用V大表示;一块小蜂窝煤的体积为πr2h,用V小表示.所以
V大=πR2H=π(2r)2·(4/3)h
=(16/3)·πr2h=(16/3)V小,
即V大∶V小=16∶3.
由上述数据,我们可以作出多种设计,如图所示,就是较为简单的两种炉膛设计.
 |
|
第8题 |
这两种炉膛内所放蜂窝煤的体积相同,能释放出同样的热量.
但是,两种炉膛内的燃烧表面积不相同,燃烧表面积大的释放热量快,火焰猛.
若不考虑蜂窝煤中间的小孔,其燃烧的表面积应该是两端底面积(煤球之间重叠不计),加上各个侧面之和,所以
S大=2πR2+3×2πRH=2π(2r)2+3×2π×2r×(4/3)h=8πr2+16πrh,
S小=2·4πr2+4·4·2πrh=8πr2+32πrh,
S小-S大=16πrh>0.
因此,小蜂窝煤在同样的体积下,燃烧的表面积大,释放热量快,即火旺些,用煤多;而用大蜂窝煤的炉灶火小些,节省煤.
9.(略).
10.(1)∵A1A⊥底面ABC,∴A1A⊥BC.
又BC⊥AC,∴BC⊥平面ACA1.
又BC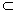 平面BCB1.∴平面ACA1⊥平面BCB1.
(2)易知∠BAC为二面角B-AA1-C的平面角.设∠BAC=θ,圆柱的底面半径为R,则
VA1-ABC=(1/3)S△ABC·A1A
=(1/3)·(1/2)AB·ACsinθ·A1A
=(1/3)·(1/2)·2R·2Rcosθsinθ·A1A
=(1/3)R2sin2θ·A1A,
V圆柱=πR2·A1A.
由题设得[(1/3)R2sin2θ·A1A]/[πR2·A1A]=(1/2
平面BCB1.∴平面ACA1⊥平面BCB1.
(2)易知∠BAC为二面角B-AA1-C的平面角.设∠BAC=θ,圆柱的底面半径为R,则
VA1-ABC=(1/3)S△ABC·A1A
=(1/3)·(1/2)AB·ACsinθ·A1A
=(1/3)·(1/2)·2R·2Rcosθsinθ·A1A
=(1/3)R2sin2θ·A1A,
V圆柱=πR2·A1A.
由题设得[(1/3)R2sin2θ·A1A]/[πR2·A1A]=(1/2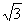 π).
∴sin2θ=(
π).
∴sin2θ=(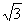 /2),故θ=30°或60°.
(3)作AD⊥A1C,垂足为D;再作DE⊥A1B,垂足为E.连结AE,易证∠AED就是二面角A-A1B-C的平面角,即∠AED=α.
∵sinα=(AD/AE),cosβ=(AC/AB),cosγ=(A1C)/(A1B),
∴?cosβ=sinαcosγ(AC/AB)=(AD/AE)·(A1C/A1B). ①
在Rt△A1AC和Rt△A1AB中,由面积关系,得
AD=(AC·A1A)/A1C,AE=(AB·A1A)/A1B.
∴(AD/AE)=(AC/A1C)·(A1B/AB)=(A1B/A1C)·(AC/AB).
∴①(AC/AB)=(A1B/A1C)·(AC/AB)·(A1C/A1B). ②
②式显然成立,从而①式成立,故
cosβ=sinαcosγ成立.
专题能力测试
一、1.C;2.A;3.B;4.A;5.C;6.B;7.D;8.C;9.A;10.D;11.D;12.C.
二、13.2π?;14.2;15.6;16.10
/2),故θ=30°或60°.
(3)作AD⊥A1C,垂足为D;再作DE⊥A1B,垂足为E.连结AE,易证∠AED就是二面角A-A1B-C的平面角,即∠AED=α.
∵sinα=(AD/AE),cosβ=(AC/AB),cosγ=(A1C)/(A1B),
∴?cosβ=sinαcosγ(AC/AB)=(AD/AE)·(A1C/A1B). ①
在Rt△A1AC和Rt△A1AB中,由面积关系,得
AD=(AC·A1A)/A1C,AE=(AB·A1A)/A1B.
∴(AD/AE)=(AC/A1C)·(A1B/AB)=(A1B/A1C)·(AC/AB).
∴①(AC/AB)=(A1B/A1C)·(AC/AB)·(A1C/A1B). ②
②式显然成立,从而①式成立,故
cosβ=sinαcosγ成立.
专题能力测试
一、1.C;2.A;3.B;4.A;5.C;6.B;7.D;8.C;9.A;10.D;11.D;12.C.
二、13.2π?;14.2;15.6;16.10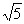 -20.
三、17.∵E是半圆周
-20.
三、17.∵E是半圆周 上一点,
∴CE⊥DE.
上一点,
∴CE⊥DE.
|
又平面DEC⊥平面ABCD |
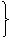 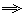 AD⊥平面DEC,且CE AD⊥平面DEC,且CE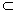 平面DEC,∴CE⊥平面ADE. 平面DEC,∴CE⊥平面ADE. |
|
AD⊥DC |
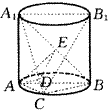
8.据《扬子晚报》报道:随着人们生活水平的提高,夜生活日趋丰富多彩,晚间的大排档(小吃)生意兴隆,这些个体户一般用两种炉灶,一个炉灶要求火旺,用于应急和炒菜,另一个炉灶火要小一点,用于慢炖、温热. 煤厂生产的蜂窝煤有两种,大蜂窝煤的直径是小蜂窝煤直径的2倍,3块大蜂窝煤垒起的高度相当于4块小蜂窝煤垒起的高度(假设不同大小的蜂窝煤,是用同样质量的煤做的). 同样质量的两种蜂窝煤,在两个炉灶中燃烧,哪一个火旺些?哪一个更节省煤? 9.在三棱锥V-ABC中,侧棱VA⊥底面ABC,∠ABC=90°. (1)求证:V、A、B、C四点在同一球面上; (2)过上述球面的球心作一平面垂直于AB,证明此平面截三棱锥所得的截面为矩形. 10.如图7-42,圆柱的轴截面为AA1B1B,C为底面圆周上一点. (1)求证:平面ACA1⊥平面BCB1;
 |
|
图7-42 |
(2)若三棱锥A1-ABC与圆柱的体积之比为1:2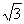 π,求二面角BAA1C的大小;
(3)设二面角A-A1B-C为α,∠CAB=β,∠CA1B=γ.求证:cosβ=sinα·cosγ.
π,求二面角BAA1C的大小;
(3)设二面角A-A1B-C为α,∠CAB=β,∠CA1B=γ.求证:cosβ=sinα·cosγ.
7.三棱锥P-ABC中,若棱PA=x,其余各棱长均为1,则x的范围是__________;三棱锥P-ABC的体积的最大值为__________. ?8.棱长为1的正方体AC1中,E、F分别是正方形A1ABB1和B1BCC1的中心.(1)求证:A1F和D1E为异面直线;(2)求异面直线A1F和D1E所成的角;(3)求三棱锥A1-EFD1的体积. ?9.空间折线ABCD中,AB、BC、CD两两垂直.(1)在以A、B、C、D为顶点的三棱锥中,写出以棱锥的各棱为棱,以棱锥的各面为面的二面角中所有的直二面角; (2)若AD与平面BCD所成的角为α,AD与平面ABC所成的角为β,求α+β的范围及二面角B-AD-C的平面角的余弦值; (3)若AD为定值a,问α、β为何值时,四棱锥ABCD的体积最大? 10.在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为D1C1与AB的中点. (1)求A1B1与截面A1ECF所成角的大小; (2)求点B到截面A1ECF的距离; (3)求截面A1ECF与底面ABCD所成角的大小.
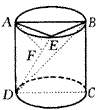
9.如图7-27,圆柱的轴截面是正方形ABCD,底面直径为2r,点E在底面圆周上,且AF⊥DE,垂足为F.若圆柱与三棱锥D-ABE的体积之比为3π,
 |
|
图7-27 |
(1)求证:AF⊥BD;
(2)求二面角A-BD-E的平面角的余弦值.
10.已知三棱锥P-ABC中,PA⊥平面ABC,BA=BC,∠ABC=90°.设二面角P-BC-A为α,二面角B-PC-A为β.求证:sinα=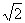 cosβ.
cosβ.
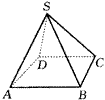
6.O是正△ABC的中心,PO⊥平面ABC.若PO=AB=a,则PA与平面ABC所成的角为_______;P到直线BC的距离为_______. 7.如图7-25,S是四边形ABCD所在平面外一点,为了推出AB⊥BC,还需要从下述条件中选出一些条件来.
 |
|
图7-25 |
①SB⊥平面ABCD;
②SC⊥CD;
③CD∥AB;
④CD∥平面SAB;
⑤BC⊥CD;
⑥CD⊥平面SBC;
⑦AB⊥平面SBC;
⑧SB⊥CD.
比如,选⑦为条件,有⑦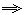 AB⊥BC;又如选③,⑤为条件,有
AB⊥BC;又如选③,⑤为条件,有
|
③ |
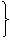 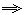 AB⊥BC.现要求推理至少用到两条定理, AB⊥BC.现要求推理至少用到两条定理, |
|
⑤ |
推理的格式为:_________.(写出两个正确的推理过程)
8.如图7-26,在梯形ABCD中,AD∥BC,∠ABC=(π/2),AB=a,AD=3a,并且∠ADC=arcsin(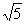 /5),又PA⊥平面ABCD,PA=a,求二面角P-CD-A的正切值.
/5),又PA⊥平面ABCD,PA=a,求二面角P-CD-A的正切值.
 |
|
图7-26 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com