
(一) 本节课的主要内容:圆的切线方程的求法;圆系方程的应用;直线与圆相交问题。
引导学生总结本节课的收获
(学生口述,师补充,共同完成)
例3.已知圆C:x2+(y-1)2=5,直线L:mx-y+1-m=0
(1)
求证m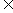 R:对直线L与圆C总有两个不同的交点A.B
R:对直线L与圆C总有两个不同的交点A.B
(2) 求A.B中点的轨迹方程
(3)
是否存在m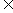 R,使以A.B为直径的圆过原点,若存在,求m的值,若不存在,说明理由.
R,使以A.B为直径的圆过原点,若存在,求m的值,若不存在,说明理由.
([点评]:这三道题主要考察学生的运算能力,应该给学生一定的做题时间.另外前两个小题的方法比较多,老师应注意收集学生不同的解法, 并且加以比较,找出最佳解法,以便统一)
([实录]:学生各抒己见,课堂气氛出现高潮:题(1)主要收集到三种方法,老师把它们进行投影:①联立方程用△>0来判断②用圆心到直线的距离d<r来判断③直线恒过定点(1,1),而(1,1)点在圆内)
师:这三种解法都很不错,说明同学们都能积极思考问题.特别注意第三种方法的技巧:当直线方程含有参数m时,我们经常把它写成m( )+( )=0形式,让两个括号都为0求定点。
([实录]:(2)学生主要有两种方法: ①利用CM⊥AB,所以KCM.K AB=-1②联立圆与直线的方程,用韦达定理求再消去m。师边投影边点评:法1其实可以用向量数量积为0来做,这样可以避免K存不存在的问题。法2 用的是参数法,它的缺陷是运算比较大,有时候参数不容易消去。)
师:有没有别的方法了?
师提示:看到垂直除了斜率乘积等于-1或者向量数量积等于0,还能想到什么?
生:圆!
师:很好,能不能用圆的方程来做这题?
([实录]:学生先独立思考一分钟,然后同桌之间相互讨论。很快得出答案:M的轨迹是以CP为直径的圆,从而得到圆的方程。师总结:法1比较好,法2运算量大,法3数形结合最简单)
(3)师提示:这是什么题型,存不存在问题。我们应先设存在。
怎样构造m的方程?式子中点的坐标用什么来处理?请同学们拿出练习本,把步骤写一写。
([点评]:本题思路简单但运算量很大,并且这个解题过程和后面的直线与圆锥曲线的解题过程异曲同工。所以要求步骤要规范统一。本题采用方式为引导思路,并且给出详细的解答过程。两个目的:本类型题目是高考的必考题,对分步得分要求严格,所以要规范步骤;另外帮助学生规范思路,解答问题的过程。需用时10分钟)
([实录]:学生思路明确,不准讨论,都动笔演算。约10分钟后,老师投影学生正确答案。点评学生的答案,表扬学生书写规范与解题严谨,给其他学生一个规范的作答。)
2、圆系方程的应用
例2.圆心为(2,1),且与已知圆x2+y2-3x=0的公共弦所在的直线过点(5,-2),求圆的方程.
师:有没有同学起来分析一下这道题,特别是不太会做的同学,可以起来说说你在哪个地方思维受阻?让别的同学帮忙解决一下。
([点评]:改变以往的授课方式,老师退出”主角”的位置,把探究问题,分析问题的主动权让给学生,鼓励学生展示自己的思维过程,这样避免了老师和学生的思维脱节,更贴近学生的实际,如果出现错误的思维过程正好暴漏学生知识的弱点)
生1:要求圆的方程应该先设圆的方程, 我知道这题与圆心有关应选择圆的标准方程.但往下不知道怎么研究两圆的公共弦所在的直线.
生2:我想到一轮复习中学过的圆系方程,圆1减圆2等于直线方程,就是两圆公共弦所在的直线方程,然后代入点求K
([实录]:师生共同活动完成这题的小结:①待定系数法求圆的方程,先根据已知条件选择方程形式:如果与圆心半径有关,用标准方程;如果告诉圆上两点或三点,用一般方程②圆系方程:(圆1)+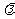 (圆2)=0 。
(圆2)=0 。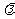
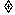 -1表示经过两圆交点的所有圆的方程;
-1表示经过两圆交点的所有圆的方程;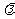 =0;表示圆1;
=0;表示圆1;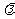 =-1表示两圆公共弦所在的直线方程(前提两圆的x2.y2两项系数要统一))
=-1表示两圆公共弦所在的直线方程(前提两圆的x2.y2两项系数要统一))
1、切线的应用
例1.(投影仪)
1) 设直线L过点A(-2,0)与圆x2+y2=1相切,则L的斜率是___________若L与圆有两个交点,则K的范围是__________________
师:(停顿2分钟)做出来请举手!并且给同学讲解一下
([点评]:鼓励学生通过思考,自己来独立解决,从而提高学生的能力。)
([实录]:一学生积极发言,投影自己的答案,并且进行讲解,不详的地方通过老师点拨或者其他同学补充)
师:很好,他用的是勾股定理,这是数形结合的方法。充分利用了圆的切线的性质,即连接圆心和切点得到垂直关系。
师:若将(-2,0)点换成(0,2)呢?
([点评]:通过设置变式,深入问题,提高学生的变通能力)
([实录]:有第一题做铺垫,学生很快作出答案,一生抢先发言,但是他第2个小题答案是(-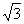 ,
,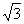 ),一部分同学有异议,说应该是(-
),一部分同学有异议,说应该是(- ,-
,-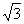 )
)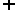 (
(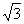 ,+
,+ )。大家开始议论,有的同学脸上写满困惑。)
)。大家开始议论,有的同学脸上写满困惑。)
师:K的范围到底是什么,不能光靠猜想。大家想一想斜率的范围应该由谁决定?
生齐答:倾斜角!
师:我们可以先来研究倾斜角,通过tan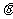 图象来直观观察K的范围。
图象来直观观察K的范围。
([实录]:学生顿悟,有的忙着画图象,有的小声议论,很快有生起来解析,并切中要害:第一个题倾斜角的范围里没有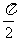 ,而第二个题有
,而第二个题有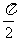 。)
。)
师:这个同学发现的非常准,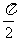 是一个特殊位置,根据角的范围求K,一定要结合tan
是一个特殊位置,根据角的范围求K,一定要结合tan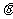 图象,看清楚K的范围到底是那些部分。
图象,看清楚K的范围到底是那些部分。
(点评:这个题目学生有明显的共同的错误就是容易弄错K的范围。针对学生出现的困惑,老师适时点拨,引导学生积极思考,而不是直接把正确做法灌输给学生,让学生自己动手挖掘答案,具体解题让学生自己完成,正确与错误方法的对照,让学生清晰的认识到自己在审题、解答过程中出现的问题)
2)
求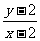 的最小值
的最小值
([点评]:改变问题形式,仍然是切线问题。通过这题复习了求切线的两种方法,设切线方程的点斜式,一种是代数方法:联立圆的方程,用△=0求K;一种是几何法,用圆心到直线的距离等于半径求K。)
师:能不能求过(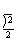 ,
,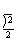 )点的切线方程?如果改成求过点P(1,2)的切线方程呢?
)点的切线方程?如果改成求过点P(1,2)的切线方程呢?
([点评]:求过一点的圆的切线方程,是圆这一章中很重要的题型。有两点要注意①是看清点是在圆上还是在圆外②是点如果在圆外,切线有两条,有时求一个K,容易只得到一条切线方程,漏掉另一条斜率不存在的切线方程。通过这道题设置问题陷阱,给容易出错的学生起到警醒的作用)
([实录]:这类题目学生很容易完成,但依然不少出错,老师让出错的同学说出答案,别的同学立即给予指正.这个同学脸上十分惭愧,从反面加深印象,起到了示范和警醒的效果)
师:投影课前小卷,附答案
[实录]:学生对照答案自己改正
[点评]:复习一轮的基础知识,并为这节课进一步深化研究直线与圆作好知识准备工作。
师:怎样判别第7题的三种位置关系?
[点评]:问题提出,导入新课,让学生明确这节课的目的和内容。
生:用圆心到直线的距离d与半径r大小进行比较:
d>r相离,d=r相切,d<r相交
师:很好,这用的是几何法,有没有别的方法要补充?
生:还可以把圆的二次方程与直线的一次方程联立,看△
△ <0相离,△=0相切,△>相交.
师:不错,这是代数法。直线和圆的位置关系非常重要,它的重要性仅次于圆锥曲线,并且是我们以后复习圆锥曲线的基础。这节课我们重点对直线和圆的位置关系进行研究。
7.直线与圆的位置关系:_______、________、________
6.圆的方程
(1)圆的标准方程:
设圆心为(a,b),半径为r,则圆的标准方程为_______,当圆心在原点时,圆的方程为_________.
(2)圆的一般方程
方程x2+y2+Dx+Ey+F =0当_______时表示圆,这叫圆的一般方程,其中圆心坐标为______,半径为________
(3)圆的直径式方程
设A(x1,y1),B(x2,y2)是圆的直径的两端点,则其直径方程为_________
5.点到直线的距离:
平面上一点P(x0,y0)到一条直线L: Ax+By+C=0的距离
d=____________________
4.两直线的位置关系:(1)两直线平行
对于直线L1:y=k1x+b1,L2:y=k2x+b2,
L1 ∥ L2
L2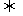 _______
_______
 (2)两直线垂直
(2)两直线垂直
对于直线L1:y=k1x+b1,L2:y=k2x+b2,
L1 ⊥ L2
L2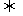 _______
_______
对于直线L1:A1x+B1y+C1=0,L2
:A2x+B2y+C2=0, L1 ⊥ L2
L2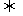 _______
_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com