
9.过点(1,)的直线l将圆 (x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时
直线l的斜率k= __
8. 若圆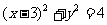 与直线
与直线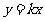 的交点分别为
的交点分别为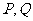 ,设
,设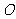 为原点
为原点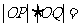 ______
______
7. 点P在直线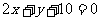 上,PA、PB与圆
上,PA、PB与圆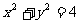 相切于A、B两点,则四边形PAOB的面积的最小值为_____
相切于A、B两点,则四边形PAOB的面积的最小值为_____
6. 在平面直角坐标系中,已知矩形ABCD的长为2,宽为1,AB、AD边分别在x轴、y轴的正半轴上,A点与坐标原点重合(如图所示).将矩形折叠,使A点落在线段DC上.
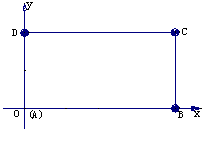 若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
若折痕所在直线的斜率为k,试写出折痕所在直线的方程;
5.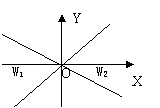 如图,直线
如图,直线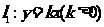 与直线
与直线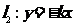 之间的阴影区域(不含边界)记为
之间的阴影区域(不含边界)记为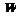 ,其左半部分记为
,其左半部分记为 ,右半部分为
,右半部分为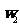 :
:
(1)分别用不等式组表示 和
和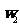 :
:
(2)若区域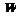 中的动点
中的动点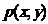 到
到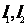 的距离之积等于
的距离之积等于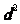 ,求点P的轨迹C的方程。
,求点P的轨迹C的方程。
(3)设不过原点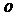 的直线
的直线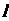 与(2)中的曲线交于
与(2)中的曲线交于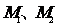 两点,且与
两点,且与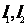 分别交于
分别交于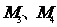 两点,求证:⊿
两点,求证:⊿ 的重心与⊿
的重心与⊿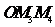 的重心重合。
的重心重合。
4.在约束条件 下,当
下,当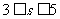 时,
时,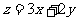 的最大值的范围是(
)
的最大值的范围是(
)
A. 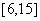 B.
B.
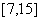 C.
C.
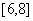 D.
D.
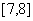
3.已知变量x,y满足约束条件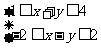 .若目标函数
.若目标函数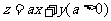 仅在点(3,1)
仅在点(3,1)
处取得最大值,则a的取值范围为__________
2.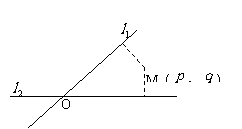 如图,平面中两条直线
如图,平面中两条直线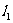 和
和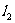 相交于点O,对于平面上任意一点M,若
相交于点O,对于平面上任意一点M,若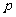 、
、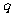 分别是M到直线
分别是M到直线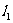 和
和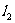 的距离,则称有序非负实数对(
的距离,则称有序非负实数对(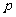 ,
,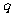 )是点M的“距离坐标”.
)是点M的“距离坐标”.
已知常数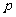 ≥0,
≥0,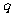 ≥0,给出下列命题:
≥0,给出下列命题:
①若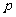 =
=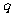 =0,则“距离坐标”为(0,0)的点有且仅有1个;
=0,则“距离坐标”为(0,0)的点有且仅有1个;
②若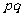 =0,且
=0,且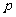 +
+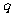 ≠0,则“距离坐标”为
≠0,则“距离坐标”为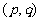 的点有且仅有2个;
的点有且仅有2个;
③若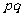 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为(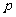 ,
,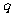 )的点
)的点
有且仅有4个.
上述命题中,正确命题的个数是( )
A 0 B 1 C 2 D 3
1.在⊿OAB中,O为坐标原点,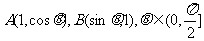 ,则当⊿OAB的面积达最大值时,
,则当⊿OAB的面积达最大值时,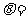 ____
____
10.设直线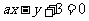 与圆
与圆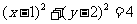 相交于
相交于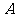 、
、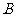 两点,且弦
两点,且弦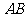 的
的
长为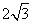 ,则
,则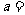 ______
______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com