
3. (2008全国Ⅱ)函数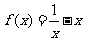 的图像关于( C )
的图像关于( C )
A.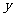 轴对称 B.
直线
轴对称 B.
直线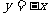 对称
对称
C. 坐标原点对称
D. 直线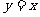 对称
对称
2.下列函数中为奇函数的是 ( C )
A. 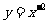 B.
B. 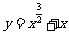
C. 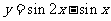 D.
D. 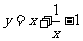
1.二次函数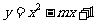 是偶函数,则函数的增区间为 ( A )
是偶函数,则函数的增区间为 ( A )
A. B.
B. C.
C. D.
D.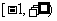
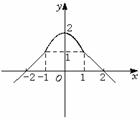
2.设 为定义在
为定义在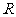 上的偶函数,当
上的偶函数,当 时,
时,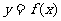 的图象是经过点
的图象是经过点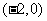 ,斜率为
,斜率为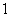 的射线,又在
的射线,又在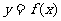 的图象中有一部分是顶点在
的图象中有一部分是顶点在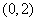 ,且过点
,且过点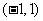 的一段抛物线
的一段抛物线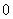 .试写出函数
.试写出函数 的表达式,并作出其图象.
的表达式,并作出其图象.
[解析]当 时,设
时,设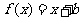 ,则由
,则由 ,即
,即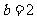 ,得
,得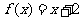 ;
;
 当
当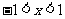 时,设
时,设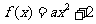 ,
,
则由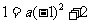 ,即
,即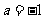 ,得
,得 ;
;
当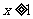 时,
时,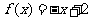 .
.
故f(x)= .
.
[题型3] 函数的周期问题
[例3] 求下列函数的周期:
(1)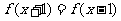 (2)
(2)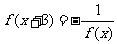
[解析](1)由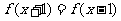 得,
得,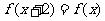 ,所以函数周期为
,所以函数周期为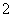
(2)由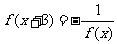 得,
得,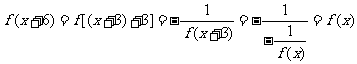 ,所以函数的周期为
,所以函数的周期为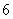 .
.
[点评]这是一个抽象函数的周期问题,注意已知等式中变量的替换,再与周期的定义结合,就可以得出周期.
[变式与拓展]
已知偶函数 是定义在
是定义在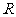 上的周期函数,其最小正周期为4.
上的周期函数,其最小正周期为4.
(1)若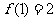 ,求
,求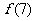 的值;
的值;
(2)若 在
在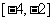 上递增,则下列关系中正确的是( )
上递增,则下列关系中正确的是( )
A.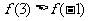 B.
B. 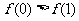
C. 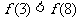 D.
D. 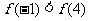
[解析](1)∵4是函数的周期,∴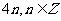 也是函数的周期.
也是函数的周期.
于是,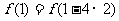
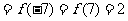 .
.
(2)偶函数在在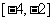 上递增,则在[2,4]上递减。由函数的最小正周期为4知,
上递增,则在[2,4]上递减。由函数的最小正周期为4知, 在[0,2]上递增。排除(B),又
在[0,2]上递增。排除(B),又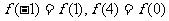 ,排除(D).
,排除(D).
∵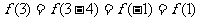 ,∴选(C).
,∴选(C).
能力训练
1.判断下列函数的奇偶性
(1)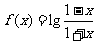
(2)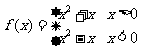
[解析](1)由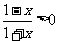 ,得
,得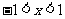 ,定义域关于原点对称,
,定义域关于原点对称,
又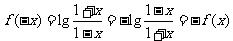 ,所以
,所以 是定义域上的奇函数.
是定义域上的奇函数.
(2)定义域为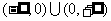 ,关于原点对称,
,关于原点对称,
又当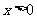 时,
时,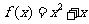 ,则
,则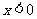 时,
时,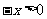 ,
,
∴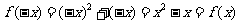 ,
,
又当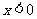 时,
时,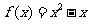 ,则
,则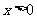 时,
时,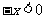 ,
,
∴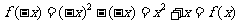 ,
,
故原函数为偶函数.
[题型2]函数奇偶性的应用
[例2]设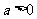 ,
,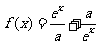 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)证明 在
在 上是增函数.
上是增函数.
[解析](1)∵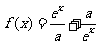 是
是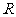 上的偶函数,∴
上的偶函数,∴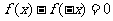 .
.
∴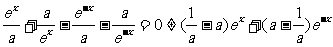
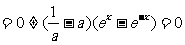
 不可能恒为“
不可能恒为“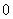 ”,∴当
”,∴当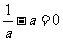 时等式恒成立,∴a=1.
时等式恒成立,∴a=1.
(2)在 上任取
上任取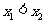 ,
,
f(x1)-f(x2)=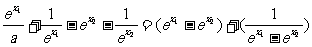
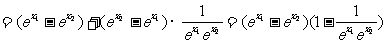
∵e>1,∴0<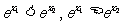 >1,∴
>1,∴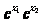 >1
>1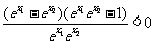 ,
,
∴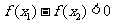 ,∴
,∴ 是在
是在 上的增函数.
上的增函数.
[点评]本题主要考查了函数的奇偶性以及单调性的基础知识.
[变式与拓展]
4.周期函数的定义:对于函数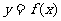 ,如果存在一个不等于
,如果存在一个不等于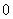 的常数
的常数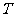 ,使得当
,使得当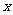 取定义域内的任意值时都有
取定义域内的任意值时都有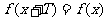 ,则
,则 是周期函数,
是周期函数,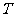 是它的一个周期.对于一个周期函数,如果所有周期中存在一个最小的正的周期,就把这个周期叫做最小正周期.
是它的一个周期.对于一个周期函数,如果所有周期中存在一个最小的正的周期,就把这个周期叫做最小正周期.
教材透析
知识点1:奇偶函数的定义域关于原点对称,解题时要优先考虑;定义域不关于原点对称的函数一定是非奇非偶函数.
知识点2:函数奇偶性的判断方法:①定义域关于原点对称;②对于奇函数若定义域中有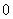 ,则
,则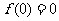 ;③ 特值检验,然后再证明;④利用某些性质:在公共定义域内,偶函数与偶函数的和(或差或积或商)是偶函数,奇函数与奇函数的和(或差或积或商)是奇函数,(作商时,注意分母不能为
;③ 特值检验,然后再证明;④利用某些性质:在公共定义域内,偶函数与偶函数的和(或差或积或商)是偶函数,奇函数与奇函数的和(或差或积或商)是奇函数,(作商时,注意分母不能为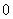 )奇函数与偶函数的积与商为奇函数.
)奇函数与偶函数的积与商为奇函数.
知识点3:函数奇偶性的应用①作函数图像;②求解析式;③奇偶性与单调性的联系:奇函数的对称区间上单调性相同,偶函数的对称区间上单调性相反;④利用奇偶性求值.
知识点4:若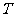 是函数的周期,则
是函数的周期,则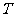 的整数倍也是函数的周期.
的整数倍也是函数的周期.
典例剖析
[题型1]判断函数的周期性
[例1](2002全国文)设函数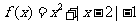 ,
,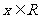 .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)求函数 的最小值.
的最小值.
[解析](1)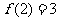 ,
,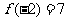
由于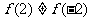 ,
,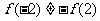
故 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)f(x)=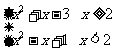 ,
,
由于 在
在 上的最小值为
上的最小值为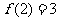 ,在
,在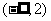 内的最小值为
内的最小值为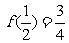 ,
,
故函数 在
在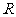 内的最小值为
内的最小值为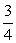 .
.
[点评]因为奇偶函数问题要紧紧抓住“任取”“都有”这两个关键词.  与
与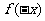 要同时有意义,f(x)与f(-x)要么相等,要么互为相反数,而要讨论非奇非偶只要说明不满足上述两点之一即可.另外,也可以借助分段函数的草图,帮助分析,然后用代数方法来回答.
要同时有意义,f(x)与f(-x)要么相等,要么互为相反数,而要讨论非奇非偶只要说明不满足上述两点之一即可.另外,也可以借助分段函数的草图,帮助分析,然后用代数方法来回答.
[变式与拓展]
3.奇、偶函数的性质
(1)具有奇偶性的函数,其定义域关于原点对称(也就是说,函数为奇函数或偶函数的必要条件是其定义域关于原点对称).
(2)奇函数的图象关于原点对称,偶函数的图象关于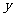 轴对称.
轴对称.
(3)若奇函数的定义域包含数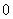 ,则
,则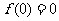 .
.
(4)奇函数的反函数也为奇函数.
(5)定义在(-∞,+∞)上的任意函数f(x)都可以唯一表示成一个奇函数与一个偶函数之和.
2.偶函数:对于函数.的定义域内任意一个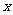 ,都有
,都有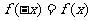
(或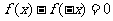 ),则称
),则称 为偶函数.
为偶函数.
1.奇函数:对于函数 的定义域内任意一个
的定义域内任意一个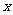 ,都有
,都有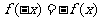
(或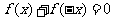 ),则称
),则称 为奇函数.
为奇函数.
12.(2006年上海春)设函数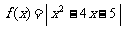 .
.
(1)在区间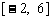 上画出函数
上画出函数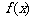 的图像;
的图像;
(2)设集合
 ,
,
试判断集合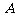 和
和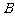 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当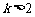 时,求证:在区间
时,求证:在区间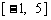 上,
上,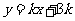 的图像位于函数
的图像位于函数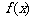 图像的上方.
图像的上方.
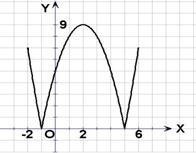
解:(1)如图所示:
(2)方程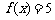 的解分别是
的解分别是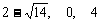 和
和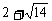 ,由于
,由于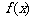 在
在 和
和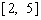 上单调递减,在
上单调递减,在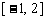 和
和 上单调递增,因此
上单调递增,因此
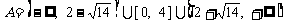 .
.
由于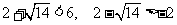 ,∴
,∴ .
.
(3)[解法一] 当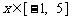 时,
时,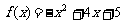 .
.
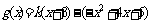
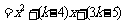
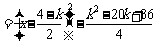 ,
,
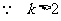 ,∴
,∴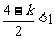 ,又
,又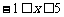 ,
,
① 当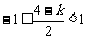 ,即
,即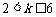 时,取
时,取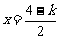 ,
,
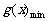
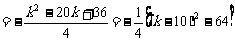 .
.
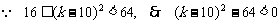 , 则
, 则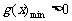 .
.
② 当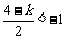 ,即
,即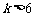 时,取
时,取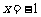 ,
, 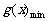 =
=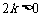 .
.
由 ①、②可知,当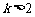 时,
时,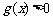 ,
,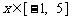 .
.
因此,在区间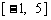 上,
上,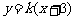 的图像位于函数
的图像位于函数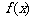 图像的上方.
图像的上方.
[解法二] 当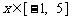 时,
时,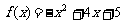 .
.
由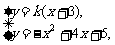 得
得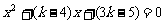 ,
,
令 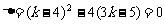 ,解得
,解得
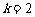 或
或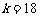 ,
,
在区间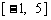 上,当
上,当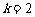 时,
时,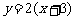 的图像与函数
的图像与函数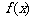 的图像只交于一点
的图像只交于一点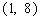 ;
当
;
当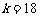 时,
时,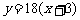 的图像与函数
的图像与函数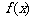 的图像没有交点.
的图像没有交点.
如图可知,由于直线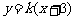 过点
过点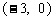 ,当
,当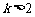 时,直线
时,直线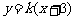 是由直线
是由直线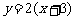 绕点
绕点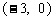 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间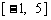 上,
上,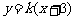 的图像位于函数
的图像位于函数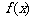 图像的上方.
图像的上方.
第三节 函数的奇偶性和周期性
自主学习
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com