
20.(本小题满分14分) 某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修.保养费用12万元,从第二年开始,每年所需维修.保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
⑴写出y与x之间的函数关系式;
⑵从第几年开始,该机床开始盈利(盈利额为正值);
⑶使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
问用哪种方案处理较为合理?请说明你的理由.
21:(本小题满分14分)已知圆C: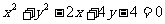 ,是否存在斜率为1的直线
,是否存在斜率为1的直线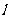 ,使
,使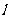 被圆C截得的弦AB为直径的圆过原点,若存在求出直线
被圆C截得的弦AB为直径的圆过原点,若存在求出直线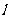 的方程,若不存在说明理由.
的方程,若不存在说明理由.
19.(本小题满分14分)已知等差数列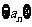 ,公差
,公差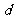 大于0,且a2、a5是方程x2-12x+27=0的两个根,数列
大于0,且a2、a5是方程x2-12x+27=0的两个根,数列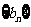 的前n 项和为Tn,且Tn=1-
的前n 项和为Tn,且Tn=1-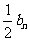 .
.
⑴求数列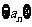 、
、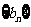 的通项公式; ⑵记
的通项公式; ⑵记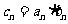 ,求证:
,求证: .
.
18.(本小题满分14分) 如图所示:四棱锥P-ABCD底面一直角
梯形,BA⊥AD,CD ⊥AD,CD=2AB,PA⊥底面ABCD,E为
PC的中点.PA= AD= AB=1.
⑴证明:EB∥平面PAD;
⑵证明:BE⊥平面PDC;
⑶求三棱锥B-PDCD的体积V.
17.(本小题满分12分) 设函数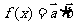 ,其中向量
,其中向量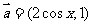 ,
,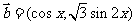 ,
,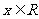 .
.
⑴若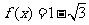 ,且
,且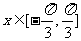 ,求
,求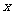 ;
;
⑵若函数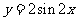 的图象按向量
的图象按向量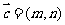 (
(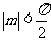 )平移后得到函数
)平移后得到函数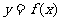 的图象,求实数
的图象,求实数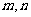 的值.
的值.

16.(本小题满分12分)由经验得知:在人民商场付款初排队等候付款的人数及其概率如下表:
|
排队人数 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
|
概率 |
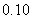 |
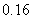 |
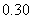 |
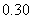 |
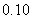 |
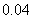 |
⑴求至多2人排队的概率;
⑵求至少2人排队的概率.
15.极坐标系内,点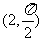 关于直线
关于直线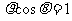 对称点的坐标为
.
对称点的坐标为
.
14.
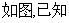 DE∥BC,△ADE
DE∥BC,△ADE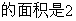 cm
cm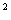 ,
,
梯形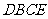
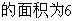 cm
cm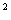 ,
,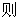
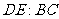
 .
.
13.关于函数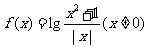 ,有下列命题:
,有下列命题:
①其图象关于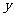 轴对称;②当
轴对称;②当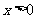 时,
时,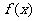 是增函数;当
是增函数;当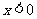 时,
时,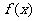 是减函数;
是减函数;
③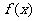 的最小值是
的最小值是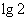 ;④当
;④当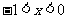 或
或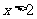 时,
时,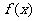 是增函数;
是增函数;
⑤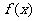 无最大值,也无最小值.
无最大值,也无最小值.
其中所有正确结论的序号是 .
▲选做题:在下面两道小题中选做一题,两道题都选的只计算第14题的得分。
12.某单位有老年人28人,中年人54人,青年人81人,为了调查他们的身体健康状况,需从他们中抽取一个容量为36的样本,抽取样本的合适方法是 .
11.已知椭圆中心在原点,一个焦点为F(-2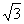 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 __________________.
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 __________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com