
21.(本小题满分12分)
解:(Ⅰ)设椭圆的右焦点为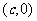 ,
,
因为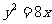 的焦点坐标为
的焦点坐标为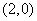 ,所以
,所以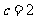 ………………………2分
………………………2分
因为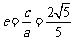 ,则
,则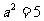 ,
,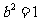
故椭圆方程为: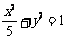 ………………………………4分
………………………………4分
(Ⅱ)由(I)得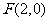 ,设
,设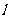 的方程为
的方程为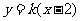 (
(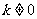 )
)
代入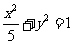 ,得
,得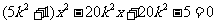 ,----------------------5分
,----------------------5分
设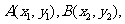 则
则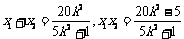 ,----------------------6分
,----------------------6分
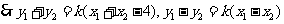
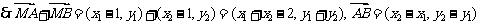
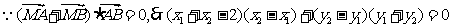 ---------8分
---------8分
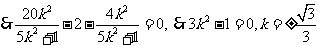 ----------------------11分
----------------------11分
所以直线 的方程为
的方程为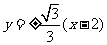 -----------------------12分
-----------------------12分
20. (本小题满分12分)
解:(Ⅰ)
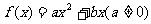 ,
,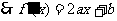
由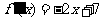 得:
得: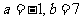 ,所以
,所以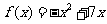 -----------------------2分
-----------------------2分
又因为点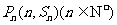 均在函数
均在函数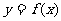 的图象上,所以有
的图象上,所以有
当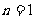 时,
时,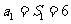
当 时,
时,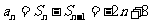 ,
,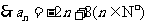 -----------------------4分
-----------------------4分
令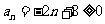 得
得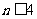 ,
,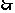 当
当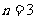 或
或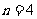 时,
时,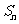 取得最大值
取得最大值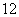
综上, 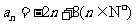 ,当
,当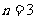 或
或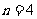 时,
时,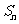 取得最大值
取得最大值 -----------------6分
-----------------6分
(Ⅱ)由题意得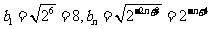 -----------------------8分
-----------------------8分
所以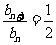 ,即数列
,即数列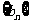 是首项为
是首项为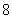 ,公比是
,公比是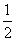 的等比数列
的等比数列
故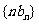 的前
的前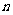 项和
项和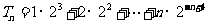 ………………①
………………①
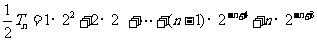 …………②
…………②
所以①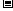 ②得:
②得: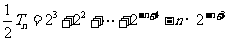 ----------------------10分
----------------------10分
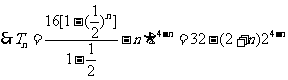 ------------------------12分
------------------------12分
19. (本小题满分12分)
解: (Ⅰ)塑胶跑道面积
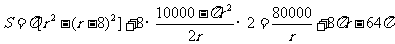 --------------------------4分
--------------------------4分
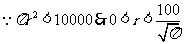 ---------------5分
---------------5分
(Ⅱ)设运动场的造价为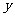 元
元
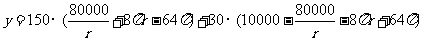
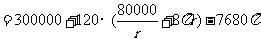 --------------------------------7分
--------------------------------7分
令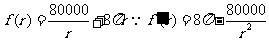 当
当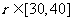 时
时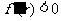
∴函数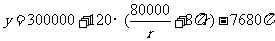 ,在
,在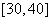 上为减函数.------10分
上为减函数.------10分
∴当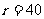 时,
时,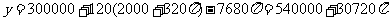 .
.
即运动场的造价最低为 元.------------------------------12分
元.------------------------------12分
18. (本题满分12分)
解:(Ⅰ) 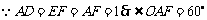 -------------------------1分
-------------------------1分
作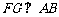 交
交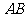 于一点
于一点 ,则
,则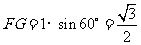 ---2分
---2分
 平面
平面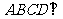 平面
平面
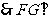 面
面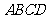 ---3分
---3分
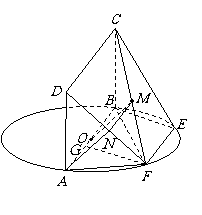 所以
所以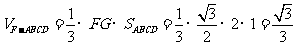 ---4分
---4分
(Ⅱ) 平面
平面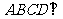 平面
平面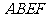 ,
,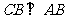 ,
,
平面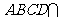 平面
平面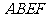 =
=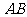 ,
,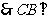 平面
平面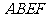 ,
,
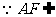 平面
平面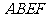 ,
,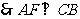 ,……… 6分
,……… 6分
又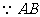 为圆
为圆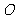 的直径,
的直径,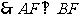 ,
,
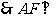 平面
平面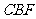 .……… 7分
.……… 7分
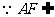 面
面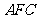 ,
,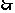 平面
平面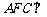 平面
平面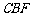 ;……… 8分
;……… 8分
(Ⅲ)取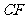 中点记作
中点记作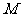 ,设
,设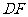 的中点为
的中点为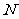 ,连接
,连接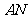 ,
,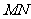
则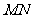
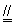
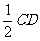 ,又
,又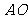
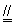
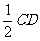 ,则
,则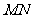
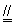
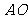 ,
,
所以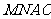 为平行四边形,
……… 10分
为平行四边形,
……… 10分
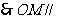
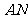 ,又
,又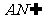 平面
平面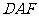 ,
,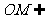 平面
平面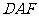 ,
,
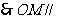 平面
平面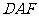 .……… 12分
.……… 12分
17.(本小题满分12分)
解:(Ⅰ)由题意得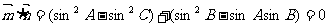
即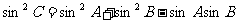 --------------------------2分
--------------------------2分
由正弦定理得 --------------------------3分
--------------------------3分
再由余弦定理得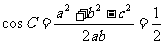
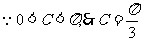 --------------------------5分
--------------------------5分
(Ⅱ)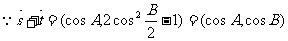 --------------------------6分
--------------------------6分
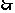
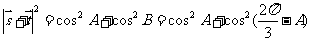
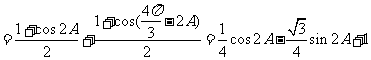 -----------------------8分
-----------------------8分
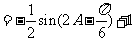 --------------------------10分
--------------------------10分
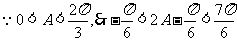
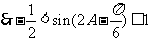
所以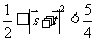 ,故
,故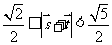 . --------------------------12分
. --------------------------12分
13.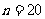 ; 14.
; 14.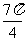 ; 15.
; 15. 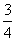
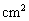 ; 16.
; 16. .
.
DABDC, BBBCC, AA
22. (本小题满分14分)
已知定义在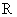 上的函数
上的函数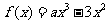 ,其中
,其中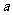 为大于零的常数.
为大于零的常数.
(Ⅰ)当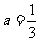 时,令
时,令 ,求证:当
,求证:当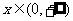 时,
时,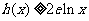 (
(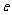 为自然对数的底数);
为自然对数的底数);
(Ⅱ)若函数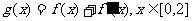 ,在
,在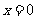 处取得最大值,求
处取得最大值,求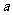 的取值范围.
的取值范围.
青岛市2010年高考模拟
数学(文科)试题答案及评分标准 2010.5
21.(本小题满分12分)
已知椭圆的方程为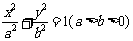 ,它的一个焦点与抛物线
,它的一个焦点与抛物线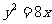 的焦点重合,离心率
的焦点重合,离心率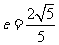 ,过椭圆的右焦点
,过椭圆的右焦点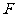 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线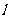 ,交椭圆于
,交椭圆于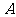 、
、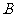 两点.
两点.
(Ⅰ)求椭圆的标准方程; (Ⅱ)设点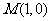 ,且
,且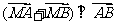 ,求直线
,求直线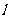 的方程;
的方程;
20. (本小题满分12分)
已知函数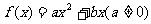 的导函数
的导函数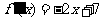 ,数列
,数列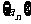 的前
的前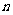 项和为
项和为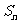 ,点
,点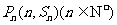 均在函数
均在函数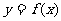 的图象上.
的图象上.
(Ⅰ)求数列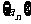 的通项公式及
的通项公式及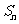 的最大值;(Ⅱ)令
的最大值;(Ⅱ)令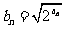 ,其中
,其中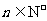 ,求
,求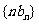 的前
的前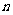 项和.
项和.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com