
6.三角函数很好地体现了对称性和周期性的关系,要把这种关系拓展到一般函数。对称性用处:对称轴和最值对应,对称点和零点对应.
5.函数的单调性是在给定的区间上考虑的,只有属于同一单调区间的两个函数值才能由它的单调性来比较大小,要注意单调区间是一个连续区间。
4.要善于将三角函数式尽可能化为只含一个三角函数的“标准式”,或者换元后成为一个初等函数式(换元后注意定义域的确定),进而可求得某些复合三角函数的最值、最小正周期、单调性等 对函数式作恒等变形时需特别注意保持定义域的不变性
对函数式作恒等变形时需特别注意保持定义域的不变性
3.单位圆中的三角函数线,是三角函数的一种几何表示,利用三角函数线进行求角和解三角不等式,有时候会更简单。
2.在已知一个角的三角函数值,求这个角的其他三角函数值时,要注意题设中角的范围,并对不同的象限分别求出相应的值 在应用诱导公式进行三角式的化简、求值时,应注意公式中符号的选取
在应用诱导公式进行三角式的化简、求值时,应注意公式中符号的选取
1.要区别正角、负角、零角、锐角、钝角、区间角、象限角、终边相同角的概念 头脑中要有一根弦:角的范围已经扩展了,系列角如何表示,相关角如何表示。
头脑中要有一根弦:角的范围已经扩展了,系列角如何表示,相关角如何表示。
15(13分)
解:(1)当 时,
时, ,
, ………… 1分
………… 1分
 ………………………………………… 2分
………………………………………… 2分
 ………………………………………… 3分
………………………………………… 3分
 …………………………………
5分
…………………………………
5分
(2) 若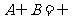 ,
, ,
, …………6分
…………6分
则 ………………………………………………………… 9分
………………………………………………………… 9分
(3)若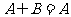 ,则
,则 ………………………………………… 10分
………………………………………… 10分
则 ………………………………………………………… 13分
………………………………………………………… 13分
16(14分)
解:(1) ………………………………… 1分
………………………………… 1分
 ……………………………………………………2分
……………………………………………………2分
(2) 令  ………………………………………… 3分
………………………………………… 3分
 ………………………………………… 4分
………………………………………… 4分
 ………………………5分
………………………5分
函数的对称轴 ,则函数在
,则函数在 上单调递增……… 6分
上单调递增……… 6分
 …………………………………………
7分
…………………………………………
7分
则函数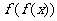 的值域为
的值域为 ……………………………… 8分
……………………………… 8分
(3)存在常数a= 满足条件,……………………………………………10分
满足条件,……………………………………………10分
∵
 ……………………………………… 12分
……………………………………… 12分
∵
 ……………………………………… 13分
……………………………………… 13分
∴ ………………………………………………14分
………………………………………………14分
17(15分)
解:(1) ,则点
,则点 ………………………………………………1分
………………………………………………1分
 ,则点
,则点 …………………………3分
…………………………3分
 ,
, …………………………5分
…………………………5分
(2)  ……………………………………6分
……………………………………6分
 …………………………………7分
…………………………………7分
 ………………10分
………………10分
(3) …………………………………………………… 11分
…………………………………………………… 11分
 …………………………………………………… 12分
…………………………………………………… 12分
 ……………………………………………………… 13分
……………………………………………………… 13分
 ……………………………………………………………… 14分
……………………………………………………………… 14分
 …………………………………………… 15分
…………………………………………… 15分
18(14分)
解:令不等式 的解集为A ,不等式
的解集为A ,不等式 的解集为B
的解集为B
则 ,
, …………………………… 4分
…………………………… 4分
(1)  ,
, …………………………………………… 5分
…………………………………………… 5分
 为真,则
为真,则 都为真命题 ……………………………………… 6分
都为真命题 ……………………………………… 6分
 ………………………………………………………………… 7分
………………………………………………………………… 7分
则 ……………………………………………………………… 8分
……………………………………………………………… 8分
则实数 的取值范围为:
的取值范围为: …………………………………… 9分
…………………………………… 9分
(2) 是
是 的充分不必要条件,等价于
的充分不必要条件,等价于 是
是 的充分不必要条件……10分
的充分不必要条件……10分
 是
是 的充分不必要条件,则
的充分不必要条件,则 是
是 的真子集………………………11分
的真子集………………………11分
 ………………………………………………………………… 12分
………………………………………………………………… 12分
则 ……………………………………………………………… 13分
……………………………………………………………… 13分
则实数 的取值范围为:
的取值范围为: …………………………………… 14分
…………………………………… 14分
19(16分)
解:(1) ………………………………………………2分
………………………………………………2分
因为 ,
, ……5分
……5分
 ……………………………………………… 6分
……………………………………………… 6分
从而 …………………………………………………7分
…………………………………………………7分
 ……………………………………………
9分
……………………………………………
9分
(2) 由(1)得 
 …………………………………… 11分
…………………………………… 11分
因为 在
在 是单调函数,则对称轴
是单调函数,则对称轴 ………12分
………12分
 …………………………………………………14分
…………………………………………………14分
 …………………………………16分
…………………………………16分
20(18分)
解:(1)因为 在
在 上是增函数
上是增函数
所以任意 ,都有
,都有 ……………………………… 2分
……………………………… 2分
又因为 未奇函数,所以
未奇函数,所以 …………………………… 3分
…………………………… 3分
任取 则
则 ………………… 4分
………………… 4分
所以 ………………………………5分
………………………………5分
所以 在
在 上是增函数……………………………………………6分
上是增函数……………………………………………6分
(2) …………………………………………………7分
…………………………………………………7分
所以 的解集为:
的解集为:  …………………… 9分
…………………… 9分
(3)由已知条件以及(2)的结果可知, ,当
,当
时恒成立,等价于 在
在 上恒成立………………………10分
上恒成立………………………10分
设 ,
,
问题转化为 在
在 恒成立………………… 11分
恒成立………………… 11分
 …………………………………………… 12分
…………………………………………… 12分
 …………………………………14分
…………………………………14分
 ……………… 16分
……………… 16分
 …………………………………………………………… 17分
…………………………………………………………… 17分
综上所述 ……………………………………………18分
……………………………………………18分
20. (本小题满分18分)
高二年级数学(文科)期中考试试卷答案及评分标准
19. (本小题满分16分)
18.(本小题满分14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com