
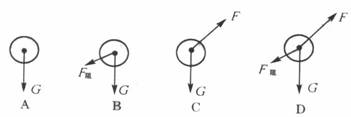
1.足球运动员已将足球踢向空中,如图所示,下列描述足球在向斜上方飞行过程中某时刻的受力图中,正确的是(G为重力,F为脚对球的作用力,F目为空气阻力) ( )

6.适当训练以平面向量为背景的解析几何问题。解析几何题中往往以向量的形式来揭示几何条件,有的要懂得看出几何特征,有的是利用坐标运算直接转化为数的关系。在解析几何中也经常利用向量解决有关角度和垂直,以及点分线段的问题,会使得问题简单化。多训练一些这样的题目,就不会感到畏惧了。
三角函数和平面向量做为高中数学的两个重要分支,内容繁杂,需要用心学习,把基础知识和基本技能练扎实,并且适当地提高能力,要把握好学习这两部分内容的度。
5.要把平面几何的性质、定理迁移到平面向量来,使得平面向量的几何推导成为可能,但题目的难度要有所控制。如:
①在平行四边形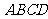 中,
中,
若 ,则
,则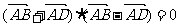 ,即菱形模型。
,即菱形模型。
若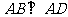 ,则
,则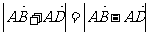 ,即矩形模型。
,即矩形模型。
②在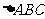 中,
中,
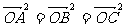 ,
,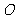 是
是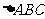 的外心;
的外心;
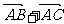 一定过
一定过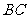 的中点;通过
的中点;通过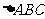 的重心;
的重心;
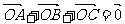 ,
,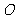 是
是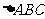 的重心;
的重心;
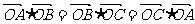 ,
,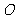 是
是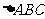 的垂心;
的垂心;

 通过
通过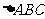 的内心;
的内心;
 则
则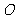 是
是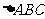 的内心;
的内心;
 .
.
4.向量的数量积运算是平面向量的重要内容,它与实数之间积的运算既有区别又联系,要辨别清楚。向量的数量积运算是采取几何运算公式还是坐标运算公式,要甄别清楚;两个公式同时运用,又可构造出一个等式。要会灵活应用向量的数量积公式求向量的模和两点间的距离。
3.向量的坐标运算使得几何问题可以通过代数运算加以解决,在对向量的几何特征掌握透彻的前提下,理解记忆相关公式。如:向量共线、垂直的充要条件,向量的数量积运算,线段定比分点公式、平移公式等。
2.先从向量的几何特征进行学习,包括向量相等,向量共线的概念,平面向量的基本定理,以及向量的加减、实数与向量的积、向量的数量积等运算的几何表示,目的是给向量建立一个系统的几何体系。
1.透彻理解向量的概念。向量概念的两大要素“方向和长度”使向量既有“形”又有“数”的特征,既联系几何又联系代数,是高中数学重要的知识网络交汇点,是数形结合的重要载体。要抱着这样的观点去学习向量知识。
9.关注三角函数在三角形中的应用,结合平面几何的性质寻找边角关系,要特别重视正弦定理和余弦定理在解三角形中的计算,掌握三角形面积公式的多种计算方法。
三角函数这部分内容在高考中的难度要求是不高的,所以在复习的时候要控制难度,但由于公式多,性质复杂,变形有一定的技巧,所以要花较多的时间加强训练,学习时注意化归思想和数形结合思想的渗透,注意易错点。
8.熟悉公式的记忆和运用
(1)诱导公式:奇变偶不变,符号看象限;
(2)两角和差的正弦、余弦、正切公式的正面运用和逆用;
(3)倍角公式以及变形,体会降幂和和差化积的意图;
(4)合一变形:asinx+bsinx=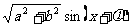 。但要控制难度,限制在
。但要控制难度,限制在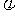 是特殊角的范围内。
是特殊角的范围内。
提醒:一些常见的变形技巧:(1)化切为弦;(2)遇公因式提取公因式;(3)凑角(不要盲目用一些公式展开,关键是看已知角和所求角有没有特殊关系。比如相差180度,90度等)
7.熟练三角函数图象的作图方法,注意定义域有限制的作图训练。通过作图去体验和巩固图象间的变换关系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com