20．(本小题满分13分)

　　　 设椭圆的左、右焦点分别为F₁、F₂，过椭圆C上的一点A作，又坐标原点O到直线AF₁的距离为

　 (1)求椭圆C的方程；

　 (2)设Q是椭圆C上的一点，过Q的直线交轴于点P(-1，0)，交轴于点M，若，求直线的方程。

19．(本小题满分13分)

　　　 某公司进行技术改造的可行性分析，在未来10年内准备向银行贷款进行技术创新。现有两种贷款方案可供选择。

　　　 方案1：一次性贷款10万元，第一年获利1万元，以后每年比前一年增加30%的利润；

　　　 方案2：每年贷款1万元，第一年获利1万元，以后每年比前一年增加5千元利润；

　　　 两种方案都是10年后一次性归还本息，若银行两种形式的贷款都按年息5%的复利计算，请你帮助该公司作出合理化选择，并说明理由。

　 (取)

18．(本小题满分12分)

　　　 如图，四边形ABCD是正方形，平面ABCD，MA//PB，PB=AB=2MA=2。

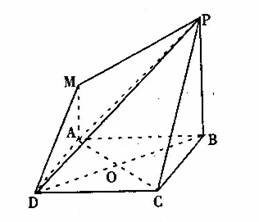　 (1)P、C、D、M四点是否在同一平面内，为什么？

　 (2)求证：面PBD 面PAC；

　 (3)求多面体PABCDM的体积。

17．(本小题满分12分)

　　　 某家政服务公司根据用户满意度将本公司家政服务员分为两类，其中A类12名、B类名。

　 (1)若采用分层抽样的方式随机抽取20名家政服务员参加技术培训，抽取到的B类人数是16，求的值；

　 (2)某客户来公司聘请3名家政服务员，但是由于公司人员安排已经接近饱和，只有甲、乙、丙、丁、戊五人可供选择，请列出该客户的所有可能选择的情况，并求该客户最终聘请了丙但没聘请乙的概率。

16．(本小题满分12分)

　　　 已知)

　 (1)求的值；

　 (2)求的值。

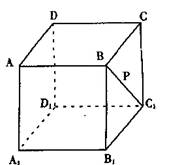
15．如图：点P在正方体ABCD-A₁B₁C₁D₁的面对角线

BC₁上运动，则下列四个命题：

　　　 ①三棱锥A-D₁PC的体积不变；

　　 ②A₁P//面ACD₁；

　　　 ③；

　　　 ④面面ACD₁。

　　　 其中正确的命题的序号是　　　　　　 。

14．在平面直角坐标系中，若不等式组(为常数)所表示的平面区域的面积被轴分成1：2两部分，则的值为　　　　 。

13．已知圆，经过点P(-1，0)的直线与圆C相切，则此直线在轴上的截距是　　　 。

12．已知数列的前项和，则数列的通项　　　　 。

11．写出函数在[0，]上的单调减区间　　　　　 。