
20.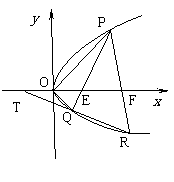 如图,设
如图,设 是抛物线
是抛物线
 上相异两点,且
上相异两点,且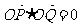 ,直线
,直线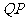 与
与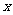 轴相交于
轴相交于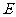 .
.
(Ⅰ)若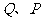 到
到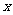 轴的距离的积为
轴的距离的积为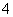 ,求该抛物线方程及
,求该抛物线方程及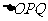 的面积的最小值.
的面积的最小值.
(Ⅱ)在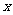 轴上是否存在一点
轴上是否存在一点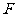 ,使直线
,使直线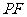 与抛物线的另一交点为
与抛物线的另一交点为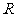 (与点
(与点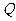 不重合),而直线
不重合),而直线 与
与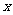 轴相交于
轴相交于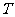 ,且有
,且有 ,若存在,求出
,若存在,求出 点的坐标(用
点的坐标(用 表示),若不存在,说明理由.
表示),若不存在,说明理由.
解:(1)∵ ,则
,则 ,
,
又 、
、 在抛物线上,故
在抛物线上,故 ,
, ,
,
故得 ,
,
 ,又
,又 ,
,
故得 ,
, .
. ,………………4分
,………………4分
设
 ,
,
直线 方程为
方程为 ,联立方程
,联立方程 ,
,
消去 得
得 ;
;
 ,
, ,
,
 ,
, 面积最小值为
面积最小值为 . ……6分
. ……6分
(Ⅱ)设 ,直线
,直线 方程为
方程为 ,联立方程组
,联立方程组 ,
,
消去 得
得 ;
;
∴ ①
①
设 ,
,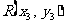 ,同理可知,
,同理可知, ②
②
由①、②可得 ③
③
若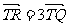 ,设
,设 ,则有
,则有 ,∴
,∴
即 ④
④
将④代入③,得 .又由(Ⅰ)知,
.又由(Ⅰ)知, ,
, ,代入①,
,代入①,
可得 ,
, .故
.故 .
.
故知,在 轴上,存在异于E的一点
轴上,存在异于E的一点 , 使得
, 使得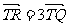 .…………12分
.…………12分
19.设函数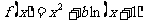 .
.
(Ⅰ)若对于定义域的任意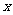 ,都有
,都有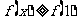 成立,求实数
成立,求实数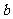 的值;
的值;
(Ⅱ)若函数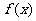 在定义域上是单调函数,求
在定义域上是单调函数,求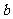 的取值范围;
的取值范围;
解(Ⅰ)由
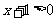 ,得
,得 ,∴
,∴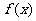 的定义域为
的定义域为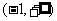 ,对
,对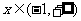 都
都
有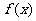 ≥
≥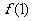 ,又函数
,又函数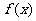 定义域上连续,∴
定义域上连续,∴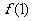 是函数
是函数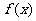 的最小值,故有
的最小值,故有
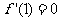 ,
,
∵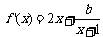 ,∴
,∴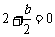 ,
,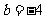 .………… 4分
.………… 4分
(Ⅱ)∵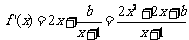 ,又函数
,又函数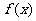 在定义域是单调函数,
在定义域是单调函数,
∴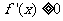 ,或
,或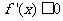 在
在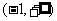 上恒成立.
上恒成立.
若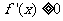 ,∵
,∵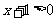 ,∴
,∴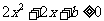 在
在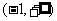 上恒成立,
上恒成立,
即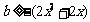
 恒成立,由此得
恒成立,由此得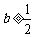 ;
;
若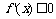 ,∵
,∵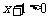 ,∴
,∴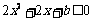 ,即
,即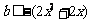 恒成立,因
恒成立,因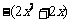 在
在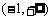 没有最小值,∴不存在实数
没有最小值,∴不存在实数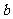 使
使 恒成立.综上所知,实数
恒成立.综上所知,实数 的取值范围
的取值范围
是 .
.
18.如图, 在平面内直线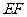 与线段
与线段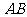 相交于
相交于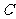 点,
点, 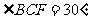 , 且
, 且
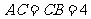 , 将此平面沿直线
, 将此平面沿直线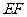 折成
折成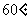 的二面角
的二面角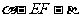 ,
,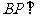 平面
平面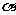 ,
,
点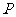 为垂足.
为垂足.
(Ⅰ) 求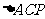 的面积;
的面积;
(Ⅱ) 求异面直线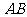 与
与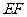 所成角的正切值.
所成角的正切值.

解:(Ⅰ) 如图, 在平面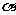 内,
过点P作PM⊥EF, 点M为垂足,
内,
过点P作PM⊥EF, 点M为垂足,
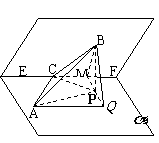 连结BM, 则∠BMP为二面角
连结BM, 则∠BMP为二面角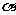 -EF-
-EF-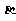 的平面角.
的平面角.
在Rt△BMC中,
由∠BCM=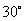 , CB = 4, 得CM
=
, CB = 4, 得CM
=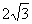 , BM=2.
, BM=2.
在Rt△BMP中,由∠BMP=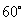 , BM=2, 得
, BM=2, 得
MP=1.在Rt△CMP中,
由CM =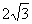 , MP=1, 得
, MP=1, 得
CP=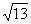 , cos∠PCM=
, cos∠PCM=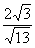 , sin∠PCM =
, sin∠PCM =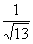 .
.
故
sin∠ACP
= sin(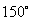 -∠PCM)=
-∠PCM)=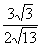 .
.
所以S△ACP=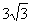 .…………………(7分)
.…………………(7分)
解:(Ⅱ) 如图, 过点A作AQ∥EF, 交MP于点Q ,
则∠BAQ是AB与EF所成的角, 且AQ⊥平面BMQ .
在△BMQ中,由∠BMQ=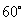 , BM=MQ=2, 得BQ = 2. …………………(10分)
, BM=MQ=2, 得BQ = 2. …………………(10分)
在Rt△BAQ中,由AQ=AC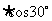 +CM
=4
+CM
=4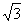 , BQ = 2, 得tan∠BAQ =
, BQ = 2, 得tan∠BAQ =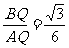 .
.
因此AB与EF所成角的正切值为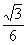 . …………………(13分)
. …………………(13分)
17.在由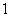 ,
,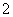 ,
,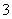 ,
,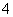 ,
,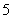 组成可重复数字的三位数中任取一个数.
组成可重复数字的三位数中任取一个数.
(Ⅰ) 求取出的数各位数字互不相同的概率;
(Ⅱ) 记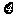 为组成这个数的各位数字中不同的偶数个数(例如:若这个数为
为组成这个数的各位数字中不同的偶数个数(例如:若这个数为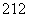 , 则
, 则
 ). 求随机变量
). 求随机变量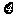 的分布列及其数学期望
的分布列及其数学期望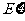 .
.
解:(Ⅰ) 记“取出的数各位数字互不相同”为事件B, 则
P(B)=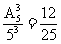 .…………………(5分)
.…………………(5分)
(Ⅱ) 随机变量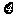 的取值为0, 1, 2.
的取值为0, 1, 2.  的分布列是
的分布列是
 |
0 |
1 |
2 |
|
P |
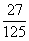 |
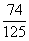 |
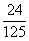 |
…………………(11分)
所以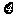 的数学期望
的数学期望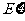 =0×
=0×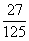 +1×
+1×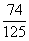 +2×
+2×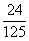 =
=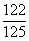 . …………………(13分)
. …………………(13分)
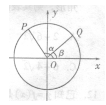
16.如图,以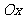 为始边作角
为始边作角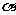 与
与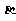 (
(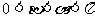 ),它们终边分别
),它们终边分别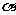 与
与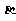
(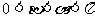 )单位圆相交于点
)单位圆相交于点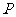 、
、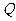 ,已知点
,已知点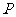 的坐标为(
的坐标为(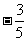 ,
,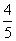 )
)
 (Ⅰ)求
(Ⅰ)求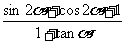 的值;
的值;
(Ⅱ)若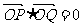 ,求
,求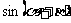 的值。
的值。
解:(Ⅰ)由三角函数定义得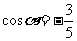 ,
,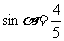 2分
2分
∴原式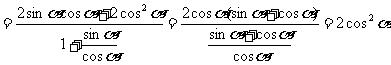 4分
4分
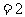 ·(
·(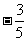 )
)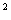 =
=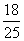 7分
7分
(Ⅱ) ·
·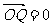 ,∴
,∴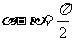 9分
9分
∴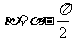 ,∴
,∴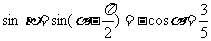
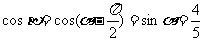 11分
11分
∴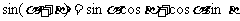
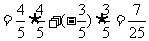 13分
13分
15.设函数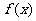 的定义域为
的定义域为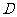 ,若存在非零实数
,若存在非零实数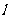 使得对于任意
使得对于任意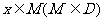 ,有
,有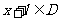 ,且
,且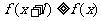 ,则称
,则称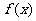 为
为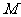 上的
上的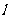 高调函数.如果定义域为
高调函数.如果定义域为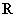 的函数
的函数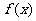 是奇函数,当
是奇函数,当 时,
时,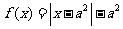 ,且
,且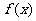 为
为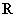 上的
上的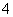 高调函数,
高调函数,
那么实数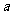 的取值范围是
的取值范围是
 .
.
14.若等比数列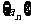 的前
的前 项和
项和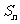 满足:
满足: 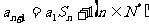 , 则
, 则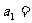
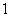 .
.
13.已知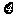 -
-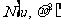 ,且
,且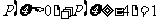 ,K^S*则
,K^S*则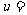
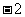 。
。
12.已知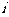 是虚数单位,函数
是虚数单位,函数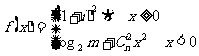 在
在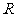 上连续,则实数
上连续,则实数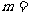
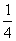 .
.
11.已知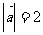 ,
,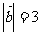 ,
,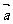 、
、 的夹角为
的夹角为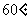 ,则
,则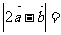
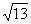 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com