
21.本题主要考查直线、椭圆的基础知识,考查函数与方程思想、分别事整合思想及化归与转化思想,满分12分。
解:(I)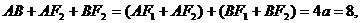
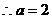 …………2分
…………2分
设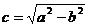 ,因为A(0,b),
,因为A(0,b),
∴直线AB的方程为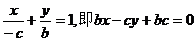 ,
,
∴点F2到直线AB的距离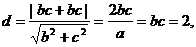 …………4分
…………4分
又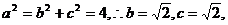
∴椭圆E的方程是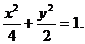 …………6分
…………6分
(II)解法一:设过点D(1,0)作两条相互垂直的直线分别与椭圆E交于P1、Q1、P2、Q2、M、N分别为P1Q1,P2Q2的中点,
当直线P1Q1的斜率不存在或为零时,P1Q1、P2Q2的中点D及原点O,直线MN为x轴
…………7分
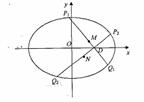 所以定点必在x轴上,
所以定点必在x轴上,
当直线的斜率存在且不为零时,
设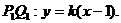
由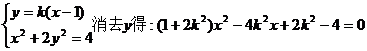
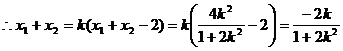 …………9分
…………9分
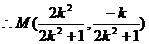
同理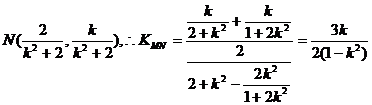
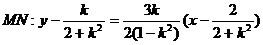
取y=0,得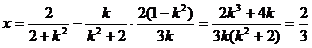 为定值。
为定值。
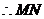 与x轴交于定点,定点坐标
与x轴交于定点,定点坐标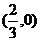 …………12分
…………12分
解法二:设过定点D(1,0)作两条互相垂直的直线分别与椭圆E交于P1、O1、P2、Q2、M、N分别为P1Q1、P2Q2的中点,
当直线的斜率存在且不为零时,设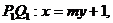
由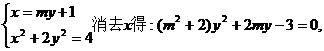
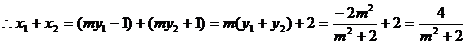
…………8分
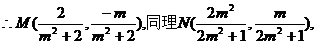
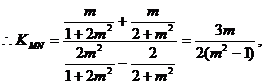
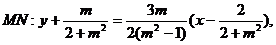
整理得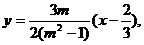
∴直线MN过定点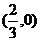 …………11分
…………11分
当直线P1Q1的斜率不存在或为零时,P1Q1、P2Q2的中点为点D及原点O,直线MN为x轴,
也过此定点,
∴直线MN过定点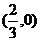 …………12分
…………12分
又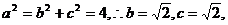
∴椭圆E的方程是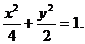 …………6分
…………6分
(II)解法一:设过点D(1,0)作两条相互垂直的直线分别与椭圆E交于P1、Q1、P2、Q2、M、N分别为P1Q1,P2Q2的中点,
当直线P1Q1的斜率不存在或为零时,P1Q1、P2Q2的中点D及原点O,直线MN为x轴
…………7分
 所以定点必在x轴上,
所以定点必在x轴上,
当直线的斜率存在且不为零时,
设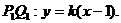
由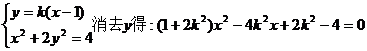
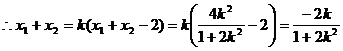 …………9分
…………9分
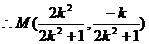
同理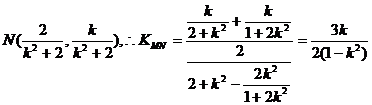
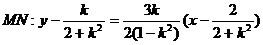
取y=0,得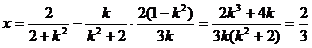 为定值。
为定值。
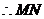 与x轴交于定点,定点坐标
与x轴交于定点,定点坐标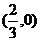 …………12分
…………12分
解法二:设过定点D(1,0)作两条互相垂直的直线分别与椭圆E交于P1、O1、P2、Q2、M、N分别为P1Q1、P2Q2的中点,
当直线的斜率存在且不为零时,设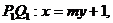
由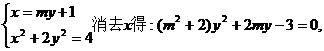
20.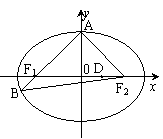 已知椭圆E:
已知椭圆E: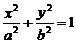 (a>b>0)的左、右焦点分别为F1、F2,A为上顶点,AF1交椭圆E于另一点B,且
(a>b>0)的左、右焦点分别为F1、F2,A为上顶点,AF1交椭圆E于另一点B,且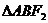 的周长为8,点F2到直线AB的距离为2。
的周长为8,点F2到直线AB的距离为2。
(I)求椭圆E的标准方程;
(II)求过D(1,0)作椭圆E的两条互相垂直的弦,M、N分别为两弦的中点,求证:直线MN经过定点,并求出定点的坐标。
19.已知函数f (x ) = lnx-ax.
(I)求f (x )的单调区间;
(II)若方程f (x ) = 0在[1,e2]上有解,求a的取值范围。
.解:
(Ⅰ)定义域为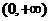
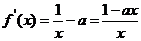 --------------------------2分
--------------------------2分
当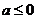 时,
时,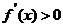 恒成立,
恒成立, 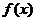 的单调递增区间为
的单调递增区间为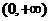 --------4分
--------4分
当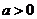 时,令
时,令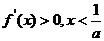
令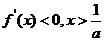
故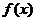 的单调递增区间为
的单调递增区间为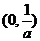 ,单调递减区间为
,单调递减区间为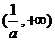 ------6分
------6分
(Ⅱ)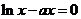 在
在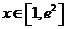 上有解,
上有解,
故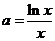 在
在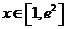 上有解
上有解
令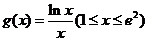
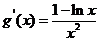 --------------------------8分
--------------------------8分
令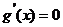 得
得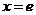
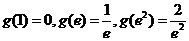
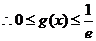
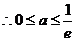 ---------------------------12分
---------------------------12分
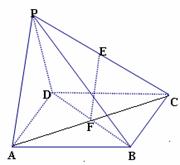
18.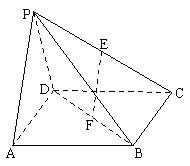 如图,在四棱锥P-ABCD中,底面ABCD是边长为
如图,在四棱锥P-ABCD中,底面ABCD是边长为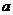 的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA = PD =
的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA = PD =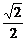 AD.
AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
(1)证明:连结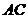 ,则
,则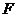 是
是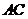 的中点,
的中点,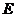 为
为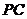 的中点,故在△
的中点,故在△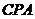 中,
中, 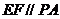 ,
…………2分
,
…………2分
且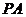
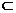 平面
平面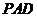 ,
,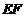
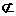 平面
平面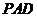 ,∴
,∴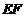 ∥平面
∥平面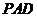 …………6分
…………6分
(2)证明:因为平面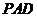 ⊥平面
⊥平面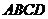 , 平面
, 平面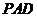 ∩平面
∩平面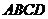 =
=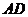 ,
,
 又
又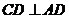 ,所以,
,所以,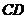 ⊥平面
⊥平面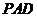 ,∴
,∴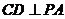 又
又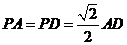 ,所以△
,所以△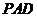 是等腰直角三角形,k.s.5.u
是等腰直角三角形,k.s.5.u
且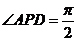 , 即
, 即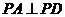 ……………9分
……………9分
又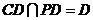 , ∴
, ∴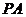 ⊥平面
⊥平面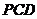 ,
,
又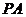
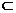 平面
平面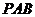 ,所以平面
,所以平面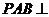 平面
平面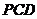 …………………12分
…………………12分
19.本题主要考查等差数列的概念及有关计算,数列求和的方法,简单分式不等式的解法,化归转化思想及运算能力等。满分12分
解:(I)(法一)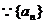 的等差数列
的等差数列
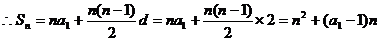 …………2分
…………2分
又由已知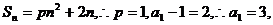 …………4分
…………4分
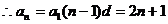
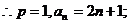 …………6分
…………6分
(法二)由已知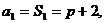
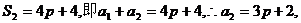 …………2分
…………2分
又此等差数列的公差为2,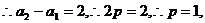
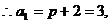 …………4分
…………4分
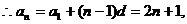
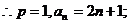 …………6分
…………6分
(法三)由已知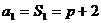 ,
,
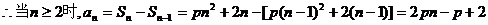
…………2分
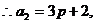
由已知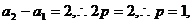 …………4分
…………4分
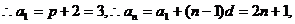
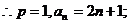 …………6分
…………6分
(II)由(I)知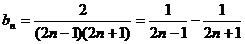 …………8分
…………8分
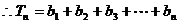
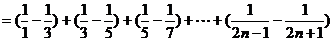
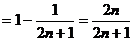 …………10分
…………10分
又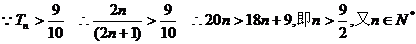
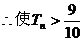 成立的最小正整数n的值为5 …………12分
成立的最小正整数n的值为5 …………12分
17.已知等差数列{an}的公差为2,其前n项和Sn = pn2 + 2n(n∈N*).
(I)求p的值及an;
(II)若bn =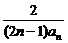 ,记数列{bn}的前n项和为Tn,求使Tn>
,记数列{bn}的前n项和为Tn,求使Tn>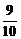 成立的最小正整数n的值.
成立的最小正整数n的值.
18.本题主要考查在实际背景下,将统计与概率相结合,考查了样本的平均数与方差的计算,以及求随机事件的概率,考查了归纳推理、应用数学知识解决实际问题的能力,满分12分。
解:(I)依题中的数据可得:
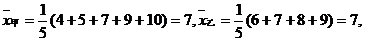
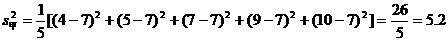
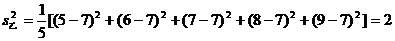
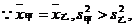
∴两组技工的总体水平相同,甲组中技工的技术水平差异比乙组大。
(II)设事件A表示:该车间“质量合格”,
则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为:
(4,5),(4,6),(4,7),(4,8),(4,9)
(5,5),(5,6),(5,7),(5,8),(5,9)
(7,5),(7,6),(7,7),(7,8),(7,9)
(9,5),(9,6),(9,7),(9,8),(9,9)
(10,5),(10,6),(10,7),(10,8),(10,9)共25种
事件A包含的基本事件为:
(4,9)
(5,8),(5,9)
(7,6),(7,7),(7,8),(7,9)
(9,5),(9,6),(9,7),(9,8),(9,9)
(10,5),(10,6),(10,7),(10,8),(10,9)共17种
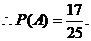
答:即该车间“质量合格”的概率为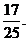
16.某车间将10名技工平均分为甲、乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
 技工
技工个数 组别 |
1号 |
2号 |
3号 |
4号 |
5号 |
|
甲组 |
4 |
5 |
7 |
9 |
10 |
|
乙组 |
5 |
6 |
7 |
8 |
9 |
(I)分别求出甲、乙两组技工在单位时间内完成合成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(II)质检部门从该车间甲、乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率。
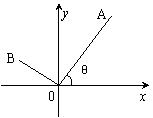
15.如图,已知A (3,4),点O为坐标原点,点B在第二象限,且|OB| = 3,记∠AOx =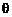 .
.
(I)求sin2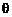 ;
;
 (II)若|AB| = 7,求sin∠Box的值.
(II)若|AB| = 7,求sin∠Box的值.
(Ⅰ)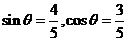
则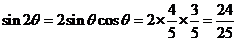
(Ⅱ)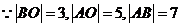
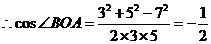
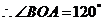
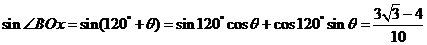
14.下列说法正确的是 . ①②④
① “x = 1”是“| x | = 1”的充分不必要条件;
② 若命题p: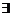 b∈R,使f (x ) = x2 + bx + 1是偶函数,则
b∈R,使f (x ) = x2 + bx + 1是偶函数,则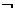 p:
p: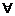 b∈R,f (x ) = x2 + bx + 1都不是偶函数;
b∈R,f (x ) = x2 + bx + 1都不是偶函数;
③ 命题“若x>a2 + b2,则x>2ab”的逆命题为真命题;
④ 因为指数函数y = ax(a>0且a≠1)是增函数(大前提),而y = (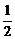 )x是指数函数(小前提),所以y = (
)x是指数函数(小前提),所以y = (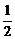 )x是增函数(结论),此推理的结论错误的原因是大前提错误.
)x是增函数(结论),此推理的结论错误的原因是大前提错误.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com