
20.(本小题满分14分)
设函数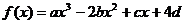 (a,b,c,d ∈R)图象关于原点对称,
(a,b,c,d ∈R)图象关于原点对称,
且x=1时,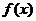 取极小值
取极小值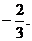
(1)求a,b,c,d的值;
(2)当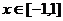 时,图象上是否存在两点,使得过此两点处的切线互相垂直?
时,图象上是否存在两点,使得过此两点处的切线互相垂直?
试证明你的结论;
(3)若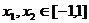 时,求证:
时,求证: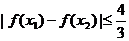 .
.

 2009-2010学年度高二第二学期期中考试(2010.4)
2009-2010学年度高二第二学期期中考试(2010.4)
19.(本小题满分14分)
某集团为了获得更大的收益,每年要投入一定的资金用于广告促销.经调查投入广告费t(百万元),
可增加销售额约为-t2+5t(百万元)(0≤t≤5).
(1)设投入广告费t(百万元),公司由此获得的收益为f(t) (百万元),
求f(t) 的表达式及其最大值; (注:收益=销售额-投入).
(2)现该公司准备共投入3百万元,分别用于广告促销和技术改造.经预测,每投入技术改造费x(百万元),可增加的销售额约为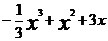 (百万元).请设计一个资金分配方案,使该公司由此获得的收益最大?
(百万元).请设计一个资金分配方案,使该公司由此获得的收益最大?
18.(本小题满分14分)
在直角坐标系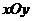 中,点 P到两点
中,点 P到两点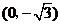 ,
,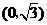 的距离之和等于4,
的距离之和等于4,
设点P的轨迹为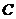 ,直线
,直线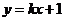 与
与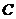 交于A,B两点.
交于A,B两点.
(1) 求点P的轨迹方程; (2)若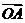
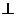
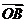 ,求k的值.
,求k的值.
17.(本小题满分14分)
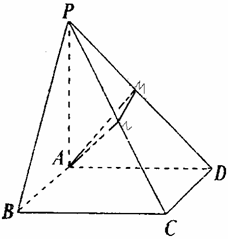
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,
PA=AD=2,点 M、N分别在棱PD、PC的中点.
(1) 求证:CD⊥PD;
(2)求证:PD⊥平面AMN;
(3)求三棱锥P-AMN的体积.
16.(本小题满分12分)
已知等差数列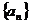 的首项
的首项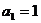 ,公差
,公差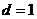 ,前
,前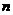 项和为
项和为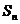 ,
,
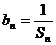
(1)求数列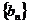 的通项公式;
的通项公式;
(2)求证: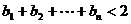
15. (本小题满分12分)
已知集合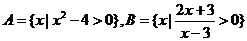
(1)求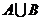 (2)求
(2)求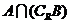 .
.
14.在约束条件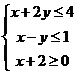 下,目标函数
下,目标函数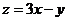 的最大值为____________
的最大值为____________
13.若抛物线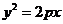 的焦点与双曲线
的焦点与双曲线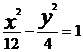 的右焦点重合,则
的右焦点重合,则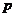 的值为_________
的值为_________
12.在等比数列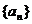 中,公比为2,前3项和为21,则
中,公比为2,前3项和为21,则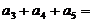 ___________
___________
11.已知向量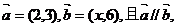 则x=
则x=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com