
020]解:(1)①CF⊥BD,CF=BD
②成立,理由如下:∵∠FAD=∠BAC=90° ∴∠BAD=∠CAF
又 BA=CA ,AD=AF ∴△BAD≌△CAF∴CF=BD ∠ACF=∠ACB=45°
∴∠BCF=90° ∴CF⊥BD ……(1分)
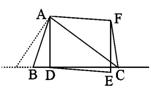 (2)当∠ACB=45°时可得CF⊥BC,理由如下:
(2)当∠ACB=45°时可得CF⊥BC,理由如下:
如图:过点A作AC的垂线与CB所在直线交于G
则∵∠ACB=45° ∴AG=AC ∠AGC=∠ACG=45°
∵AG=AC AD=AF ………(1分)
∴△GAD≌△CAF(SAS) ∴∠ACF=∠AGD=45°
∴∠GCF=∠GCA+∠ACF=90° ∴CF⊥BC …………(2分)
(3)如图:作AQBC于Q
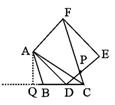 ∵∠ACB=45° AC=4
∵∠ACB=45° AC=4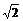 ∴CQ=AQ=4
∴CQ=AQ=4
∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°
∴△ADQ∽△DPC …(1分)
∴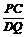 =
=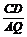
设CD为x(0<x<3)则DQ=CQ-CD=4-x则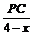 =
=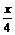 …………(1分)
…………(1分)
∴PC=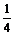 (-x2+4x)=-
(-x2+4x)=-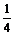 (x-2)2+1≥1
(x-2)2+1≥1
当x=2时,PC最长,此时PC=1 ………(1分)
019](1)EO>EC,理由如下:
由折叠知,EO=EF,在Rt△EFC中,EF为斜边,∴EF>EC, 故EO>EC …2分
(2)m为定值
∵S四边形CFGH=CF2=EF2-EC2=EO2-EC2=(EO+EC)(EO―EC)=CO·(EO―EC)
S四边形CMNO=CM·CO=|CE―EO|·CO=(EO―EC) ·CO
∴ ……………………………………………………4分
……………………………………………………4分
(3)∵CO=1,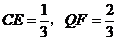 ∴EF=EO=
∴EF=EO=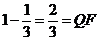
∴cos∠FEC=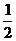 ∴∠FEC=60°,
∴∠FEC=60°,
∴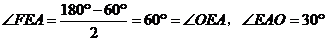
∴△EFQ为等边三角形,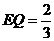 …………………………………………5分
…………………………………………5分
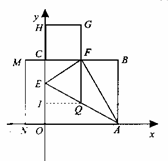
作QI⊥EO于I,EI=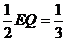 ,IQ=
,IQ=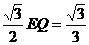
∴IO=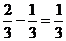 ∴Q点坐标为
∴Q点坐标为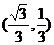 ……………………………………6分
……………………………………6分
∵抛物线y=mx2+bx+c过点C(0,1), Q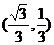 ,m=1
,m=1
∴可求得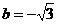 ,c=1
,c=1
∴抛物线解析式为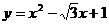 ……………………………………7分
……………………………………7分
(4)由(3),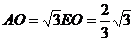
 当
当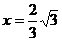 时,
时,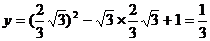 <AB
<AB
∴P点坐标为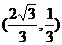 …………………8分
…………………8分
∴BP=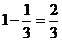 AO
AO
方法1:若△PBK与△AEF相似,而△AEF≌△AEO,则分情况如下:
①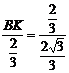 时,
时,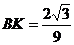 ∴K点坐标为
∴K点坐标为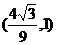 或
或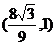
②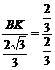 时,
时,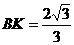 ∴K点坐标为
∴K点坐标为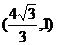 或
或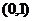 …………10分
…………10分
故直线KP与y轴交点T的坐标为
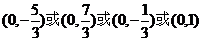 …………………………………………12分
…………………………………………12分
方法2:若△BPK与△AEF相似,由(3)得:∠BPK=30°或60°,过P作PR⊥y轴于R,则∠RTP=60°或30°
①当∠RTP=30°时,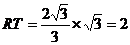
②当∠RTP=60°时,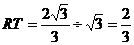
∴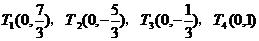 ……………………………12分
……………………………12分
018]解:(1)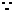 抛物线
抛物线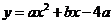 经过
经过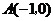 ,
,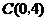 两点,
两点,
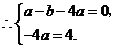 解得
解得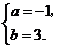
 抛物线的解析式为
抛物线的解析式为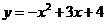 .
.
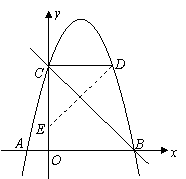 (2)
(2) 点
点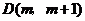 在抛物线上,
在抛物线上,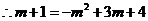 ,
,
即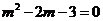 ,
,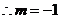 或
或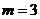 .
.
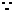 点
点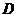 在第一象限,
在第一象限, 点
点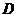 的坐标为
的坐标为 .
.
由(1)知 .
.
设点 关于直线
关于直线 的对称点为点
的对称点为点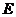 .
.
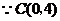 ,
,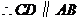 ,且
,且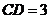 ,
,
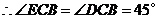 ,
,
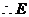 点在
点在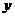 轴上,且
轴上,且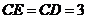 .
.
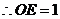 ,
,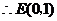 .
.
即点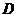 关于直线
关于直线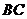 对称的点的坐标为(0,1).
对称的点的坐标为(0,1).
(3)方法一:作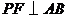 于
于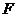 ,
, 于
于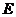 .
.
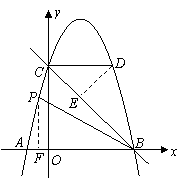 由(1)有:
由(1)有: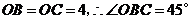 ,
,
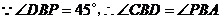 .
.
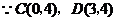 ,
,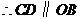 且
且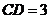 .
.
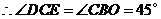 ,
,
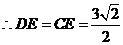 .
.
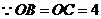 ,
,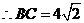 ,
,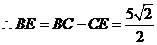 ,
,
 .
.
设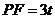 ,则
,则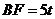 ,
,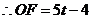 ,
,
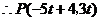 .
.
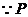 点在抛物线上,
点在抛物线上,

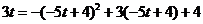 ,
,
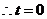 (舍去)或
(舍去)或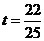 ,
,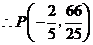 .
.
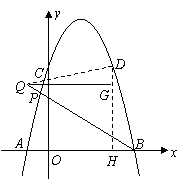 方法二:过点
方法二:过点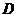 作
作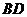 的垂线交直线
的垂线交直线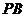 于点
于点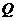 ,过点
,过点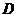 作
作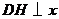 轴于
轴于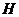 .过
.过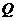 点作
点作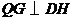 于
于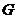 .
.
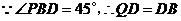 .
.
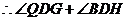
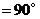 ,
,
又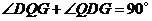 ,
,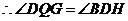 .
.
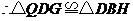 ,
,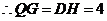 ,
,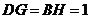 .
.
由(2)知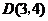 ,
,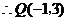 .
.
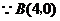 ,
, 直线
直线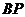 的解析式为
的解析式为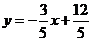 .
.
解方程组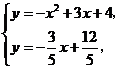 得
得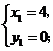
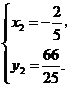
 点
点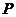 的坐标为
的坐标为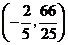 .
.
017]解:(1)已知抛物线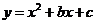 经过
经过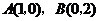 ,
,
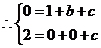 解得
解得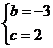
 所求抛物线的解析式为
所求抛物线的解析式为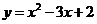 .··································································· 2分
.··································································· 2分
(2)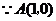 ,
,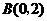 ,
,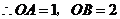
可得旋转后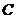 点的坐标为
点的坐标为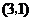 ······················································································ 3分
······················································································ 3分
当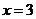 时,由
时,由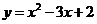 得
得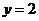 ,
,
可知抛物线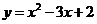 过点
过点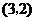
 将原抛物线沿
将原抛物线沿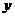 轴向下平移1个单位后过点
轴向下平移1个单位后过点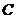 .
.
 平移后的抛物线解析式为:
平移后的抛物线解析式为: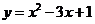 .···························································· 5分
.···························································· 5分
(3)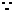 点
点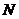 在
在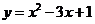 上,可设
上,可设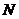 点坐标为
点坐标为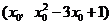
将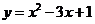 配方得
配方得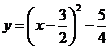 ,
, 其对称轴为
其对称轴为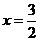 .······························ 6分
.······························ 6分
 ①当
①当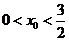 时,如图①,
时,如图①,
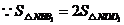
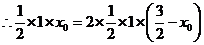
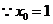
此时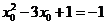

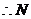 点的坐标为
点的坐标为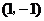 .····························································································· 8分
.····························································································· 8分
②当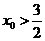 时,如图②
时,如图②
同理可得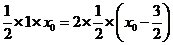
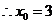
此时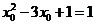
 点
点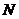 的坐标为
的坐标为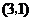 .
.
综上,点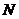 的坐标为
的坐标为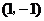 或
或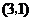 .········································································· 10分
.········································································· 10分
016]解:(1)设正比例函数的解析式为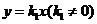 ,
,
因为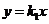 的图象过点
的图象过点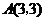 ,所以
,所以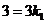 ,解得
,解得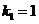 .
.
这个正比例函数的解析式为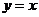 .······································································· (1分)
.······································································· (1分)
设反比例函数的解析式为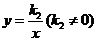 .因为
.因为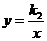 的图象过点
的图象过点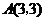 ,所以
,所以
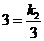 ,解得
,解得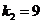 .这个反比例函数的解析式为
.这个反比例函数的解析式为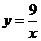 .··································· (2分)
.··································· (2分)
(2)因为点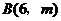 在
在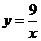 的图象上,所以
的图象上,所以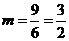 ,则点
,则点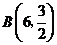 .········ (3分)
.········ (3分)
设一次函数解析式为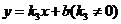 .因为
.因为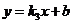 的图象是由
的图象是由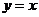 平移得到的,
平移得到的,
所以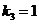 ,即
,即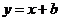 .又因为
.又因为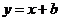 的图象过点
的图象过点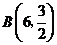 ,所以
,所以
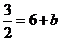 ,解得
,解得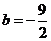 ,
, 一次函数的解析式为
一次函数的解析式为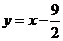 .······························ (4分)
.······························ (4分)
(3)因为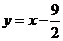 的图象交
的图象交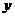 轴于点
轴于点 ,所以
,所以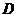 的坐标为
的坐标为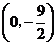 .
.
设二次函数的解析式为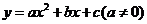 .
.
因为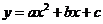 的图象过点
的图象过点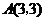 、
、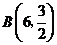 、和
、和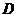
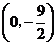 ,
,
所以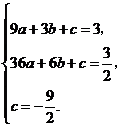 ··················· (5分)
解得
··················· (5分)
解得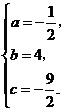
这个二次函数的解析式为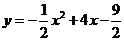 .····················································· (6分)
.····················································· (6分)
(4)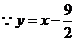 交
交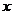 轴于点
轴于点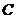 ,
, 点
点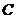 的坐标是
的坐标是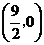 ,
,
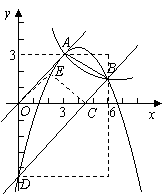 如图所示,
如图所示,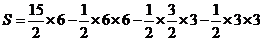
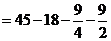
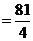 .
.
假设存在点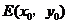 ,使
,使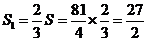 .
.
 四边形
四边形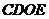 的顶点
的顶点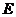 只能在
只能在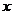 轴上方,
轴上方,
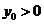 ,
,

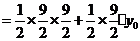
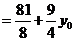 .
.
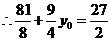 ,
,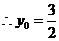 .
.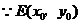 在二次函数的图象上,
在二次函数的图象上,
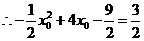 .解得
.解得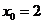 或
或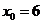 .
.
当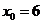 时,点
时,点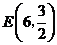 与点
与点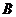 重合,这时
重合,这时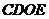 不是四边形,故
不是四边形,故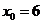 舍去,
舍去,
 点
点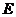 的坐标为
的坐标为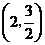 . (8分)
. (8分)
015]⑴设二次函数的解析式为:y=a(x-h)2+k∵顶点C的横坐标为4,且过点(0,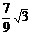 )
)
∴y=a(x-4)2+k 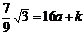 ………………①
………………①
又∵对称轴为直线x=4,图象在x轴上截得的线段长为6 ∴A(1,0),B(7,0)
∴0=9a+k
………………②由①②解得a=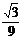 ,k=
,k=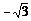 ∴二次函数的解析式为:y=
∴二次函数的解析式为:y=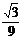 (x-4)2-
(x-4)2-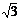
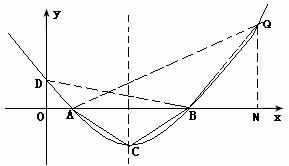
⑵∵点A、B关于直线x=4对称 ∴PA=PB ∴PA+PD=PB+PD≥DB ∴当点P在线段DB上时PA+PD取得最小值 ∴DB与对称轴的交点即为所求点P
设直线x=4与x轴交于点M ∵PM∥OD,∴∠BPM=∠BDO,又∠PBM=∠DBO
∴△BPM∽△BDO∴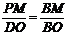 ∴
∴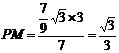 ∴点P的坐标为(4,
∴点P的坐标为(4,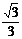 )
)
⑶由⑴知点C(4,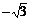 ),又∵AM=3,∴在Rt△AMC中,cot∠ACM=
),又∵AM=3,∴在Rt△AMC中,cot∠ACM=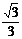 ,
,
∴∠ACM=60o,∵AC=BC,∴∠ACB=120o
①当点Q在x轴上方时,过Q作QN⊥x轴于N 如果AB=BQ,由△ABC∽△ABQ有
BQ=6,∠ABQ=120o,则∠QBN=60o ∴QN=3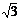 ,BN=3,ON=10,此时点Q(10,
,BN=3,ON=10,此时点Q(10,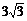 ),
),
如果AB=AQ,由对称性知Q(-2,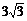 )
)
②当点Q在x轴下方时,△QAB就是△ACB,此时点Q的坐标是(4,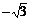 ),
),
经检验,点(10,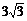 )与(-2,
)与(-2,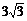 )都在抛物线上
)都在抛物线上
综上所述,存在这样的点Q,使△QAB∽△ABC
点Q的坐标为(10,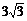 )或(-2,
)或(-2,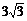 )或(4,
)或(4,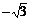 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com