6．(原创)1856年“石达开增援西征军，在鄱阳湖打败了湘军水师，进军江西，迅速占领许多州县。至此，太平天国夺取了清朝的半壁江山，太平天国进入全盛时期。”下列对“太平天国夺取了清朝的半壁江山”的理解正确的是(　　　 )

A.占领了清朝的一半左右的领土　　　　

B.占领了清朝的中心区域--黄河流域和长江流域

C.占领了清朝长江中下游流域，其经济地位重要　　

D.占领的整个长江流域占一半左右的领土又是经济中心

5．君主立宪制下的英国国王和美国总统都可以进行的政治活动是　

A.否决议会(国会)制定的法律　 B.处理国家重大事务和日常事务

C.代表国家参与外交活动　 　 D.当与议会发生矛盾时有权解散议会

4．在举行公民集会的那天，所有的男性公民纷纷涌向一个公共场所，在那里选举与罢免公职人员，并决定是否判处某个公民的死刑，这样的场所应是

A.罗马的元老院　　　　　　　　 B.雅典的广场　　

C.美国的国会山　　　　　　　　 D.英国的法院

3．在宋代的官员中，有三分之一以上来自平民家庭，这是因为当时推行的选官制度是

A．军功爵制　　　　　　　　　 B．察举制　　　　

C．九品中正制　　　　　　　　 D．科举制

2．①春秋时期，郑国发生了火灾，掌管祭祀的官员建议子产焚烧玉石向上天祈祷，②子产说：“天道远，人道迩，非所及也。”③于是积极组织灭火。④这说明当时以祭祀为核心的宗教意识日益淡薄，而世俗理性逐渐占据上风。上述材料中属于历史评价的是A．①　　　　 B．②　　　　　 C．③　　　　　 D．④

1．某地洪水为患，消息上报朝廷后，皇帝一方面交代工部尽快抢修溃决的堤防，勿使水患继续扩大；另一方面责成户部尽快调度粮食，运往灾区，赈济灾民。幕僚根据皇帝之意，写成诏书，经皇帝确认无误后，直接送至工部、户部等单位执行。这是下列哪个时期的制度 　　　　　　A．秦汉 　　　　　　　　B．隋唐 　　　

C．宋元 　　　　　　　　D．明清

(三)解答题

14、已知y=2x是△ABC中∠C平分线所在直线方程，A(-4，2)，B(3，1)，求点C坐标，并判断△ABC形状。

15、已知n条直线：x-y+c_i=0(i=1，2，…，n)，其中C₁=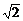，C₁<C₂<C₃<…<C_n，且每相邻两条之间的距离顺次为2，3，4，…，n，(1)求C_n；(2)求x-y+C_n=0与坐标轴围成的三角形面积：(3)求x-y+C_n-1=0与x-y+C_n=0与x轴、y轴围成的图形面积。

16、已知与曲线C：x²+y²-2x-2y+1=0相切的直线l交x、y轴于A、B两点，O为原点，|OA|=a，|OB|=b，a>2，b>2，(1)求证：(a-2)(b-2)=2；(2)求线段AB中点的轨迹方程；(3)求△AOB面积的最小值。

17、已知两圆x²+y²=4和x²+(y-8)²=4，(1)若两圆分别在直线y=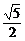x+b两侧，求b取值范围；(2)求过点A(0，5)且和两圆都没有公共点的直线的斜率k的范围。

18、当0<a<2时，直线l₁：ax-2y-2a+4=0与l₂：2x+a²y-2a²-4=0和坐标轴成一个四边形，要使围成的四边形面积最小，a应取何值？

(二)填空题

　　 9、直线ax+by+c=0与直线dx+ey+c=0的交点为(3，-2)，则过点(a，b)，(d，e)的直线方程是___________________。

10、已知{(x，y)|(m+3)x+y=3m-4}∩{(x，y)|7x+(5-m)y-8=0}=φ，则直线(m+3)x+y=

3m+4与坐标轴围成的三角形面积是__________________。

11、已知x，y满足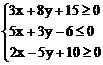，则x-y的最大值为________，最小值为________。

12、过点A(2，1)，且在坐标轴截距相等的直线方程是_________________。

13、已知圆：(x-1)²+y²=1，作弦OA，则OA中点的轨迹方程是__________________。

(一)选择题

1、若直线(m²-1)x-y+1-2m=0不过第一象限，则实数m取值范围是

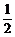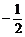A、-1<m≤　　　 B、≤m≤1　　 C、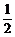<m<1　　　 D、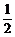≤m≤1

2、已知直线2x+y-2=0和mx-y+1=0的夹角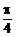为，则m值为

A、　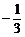 或-3　　　 B、-3或　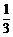　　　 C、-3或3　　　　 D、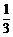或3

3、点P在直线x+y-4=0上，O为原点，则|OP|的最小值是

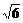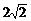A、　 2　　　　　　 B、　　　　　　 C、 　　　　　D、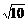

4、过点A(1，4)，且横纵截距的绝对值相等的直线共有

A、　 1条　　　　　 B、2条　　　　　 C、3条　　　　　 D、4条

5、圆x²+y²-4x+2y+C=0与y轴交于A、B两点，圆心为P，若∠APB=90⁰，则C的值是

A、　 -3　　　　　 　B、3　　　　　　 C、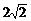　　　　　 D、8

　　 6、若圆(x-3)²+(y+5)²=r²上有且只有两个点到直线4x-3y-2=0距离等于1，则半径r取值范围是

A、　 (4，6)　　　 B、[4，6)　　　　 C、(4，6]　　　　 D、[4，6]

　　 7、将直线x+y-1=0绕点(1，0)顺时针旋转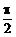后，再向上平移一个单位，此时恰与圆x²+(y-1)²=R²相切，则正数R等于

A、　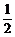 　　　　　　　B、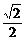　　　　　 C、1　　　　 　　　D、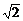

8、　 方程x²+y²+2ax-2ay=0所表示的圆

A、关于x轴对称　　　　　　　　　　 B、关于y轴对称

C、关于直线x-y=0对称　　　　　　　 D、关于直线x+y=0对称

例1、已知定点P(6，4)与定直线l₁：y=4x，过P点的直线l与l­₁交于第一象限Q点，与x轴正半轴交于点M，求使△OQM面积最小的直线l方程。

分析：

直线l是过点P的旋转直线，因此是选其斜率k作为参数，还是选择点Q(还是M)作为参数是本题关键。

通过比较可以发现，选k作为参数，运算量稍大，因此选用点参数。

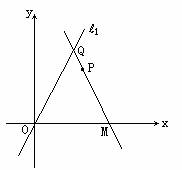设Q(x₀，4x₀)，M(m，0)

∵ Q，P，M共线

∴ k_PQ=k_PM

∴

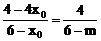
解之得：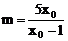

∵ x₀>0，m>0

∴ x₀-1>0

∴

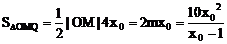
令x₀-1=t，则t>0

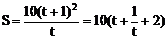　 ≥40

当且仅当t=1，x₀=11时，等号成立

此时Q(11，44)，直线l：x+y-10=0

评注：本题通过引入参数，建立了关于目标函数S_△OQM的函数关系式，再由基本不等式再此目标函数的最值。要学会选择适当参数，在解析几何中，斜率k，截距b，角度θ，点的坐标都是常用参数，特别是点参数。

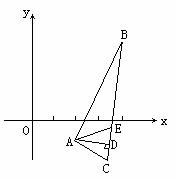
例2、已知△ABC中，A(2，-1)，B(4，3)，C(3，-2)，求：

　 (1)BC边上的高所在直线方程；(2)AB边中垂线方程；(3)∠A平分线所在直线方程。

分析：

　 (1)∵ k_BC=5

∴ BC边上的高AD所在直线斜率k=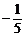

∴ AD所在直线方程y+1=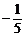(x-2)

即x+5y+3=0

　 (2)∵ AB中点为(3，1)，k_AB=2

∴ AB中垂线方程为x+2y-5=0

　 (3)设∠A平分线为AE，斜率为k，则直线AC到AE的角等于AE到AB的角。

∵ k_AC=-1，k_AB=2

∴

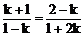
∴ k²+6k-1=0

∴ k=-3-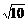(舍)，k=-3+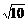

∴ AE所在直线方程为(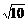-3)x-y-2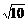+5=0

评注：在求角A平分线时，必须结合图形对斜率k进行取舍。一般地涉及到角平分线这类问题时，都要对两解进行取舍。也可用轨迹思想求AE所在直线方程，设P(x，y)为直线AE上任一点，则P到AB、AC距离相等，得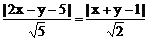，化简即可。还可注意到，AB与AC关于AE对称。

例3、(1)求经过点A(5，2)，B(3，2)，圆心在直线2x-y-3=0上圆方程；

　 (2)设圆上的点A(2，3)关于直线x+2y=0的对称点仍在这个圆上，且与直线x-y+1=0相交的弦长为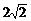，求圆方程。

分析：

研究圆的问题，既要理解代数方法，熟练运用解方程思想，又要重视几何性质及定义的运用，以降低运算量。总之，要数形结合，拓宽解题思路。

(1)法一：从数的角度

若选用标准式：设圆心P(x，y)，则由|PA|=|PB|得：(x₀-5)²+(y₀-2)²=(x₀-3)²+(y₀-2)²

又2x₀-y₀-3=0

两方程联立得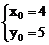：，|PA|=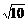

∴ 圆标准方程为(x-4)²+(y-5)²=10

若选用一般式：设圆方程x²+y²+Dx+Ey+F=0，则圆心()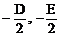

∴

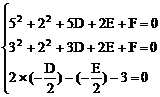
解之得：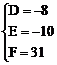

法二：从形的角度

AB为圆的弦，由平几知识知，圆心P应在AB中垂线x=4上，则由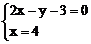得圆心P(4，5)

∴ 半径r=|PA|=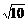

显然，充分利用平几知识明显降低了计算量

(2)设A关于直线x+2y=0的对称点为A’

由已知AA’为圆的弦

∴ AA’对称轴x+2y=0过圆心

设圆心P(-2a，a)，半径为R

则R=|PA|=(-2a-2)²+(a-3)²

又弦长，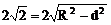

∴

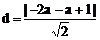
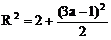
∴ 4(a+1)²+(a-3)²=2+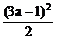

∴ a=-7或a=-3

当a=-7时，R=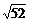；当a=-3时，R=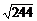

∴ 所求圆方程为(x-6)²+(y+3)²=52或(x-14)²+(y+7)²=244

例4、已知方程x²+y²-2(m+3)x+2(1-4m²)y+16m⁴+9=0表示一个圆，(1)求实数m取值范围；(2)求圆半径r取值范围；(3)求圆心轨迹方程。

分析：

　 (1)m满足[-2(m+3)]²+[2(1-4m²)]²-4(16m⁴+9)>0，即7m²-6m-1<0

∴

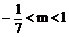
(3)半径r=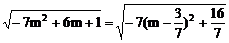

　∵

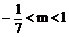
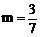　∴ 时，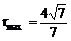

　∴ 0<r≤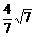

　 (3)设圆心P(x，y)，则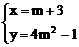

消去m得：y=4(x-3)²-1

又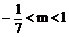

∴

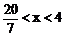
∴ 所求轨迹方程为(x-3)²=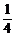(y+1)()

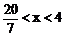例5、如图，过圆O：x²+y²=4与y轴正半轴交点A作此圆的切线l，M为l上任一点，过M作圆O的另一条切线，切点为Q，求△MAQ垂心P的轨迹方程。

分析：

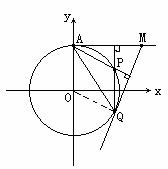从寻找点P满足的几何条件着手，着眼于平几知识的运用。

连OQ，则由OQ⊥MQ，AP⊥MQ得OQ∥AP

同理，OA∥PQ

又OA=OQ

∴ OAPQ为菱形

∴ |PA|=|OA|=2

设P(x，y)，Q(x₀，y₀)，则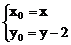

又x₀²+y₀²=4

∴ x²+(y-2)²=4(x≠0)

评注：一般说来，当涉及到圆的切线时，总考虑过焦点的弦与切线的垂直关系；涉及到圆的弦时，常取弦的中点，考虑圆心、弦的中点、弦的端点组成的直角三角形。

同步练习