
21、(共14分)
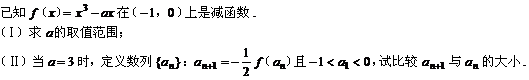
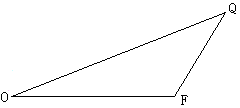
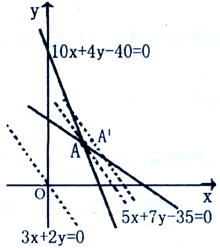
20、解:
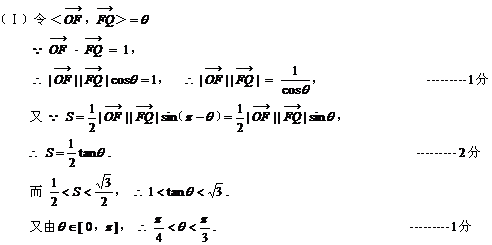
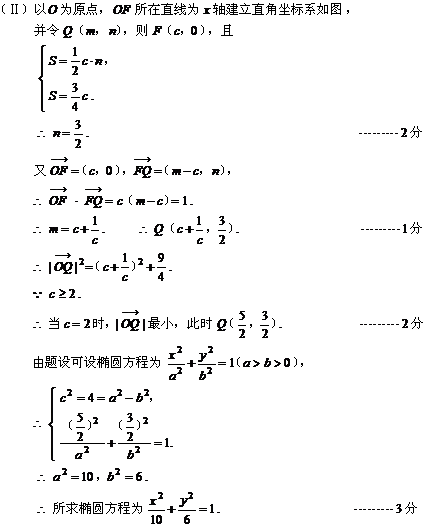
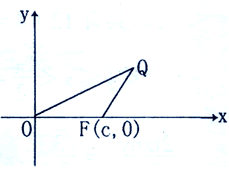
20、(共12分)
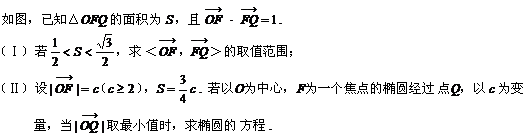
19、(共12分)
医院用甲、乙两种药片为手术后的病人配营养餐. 已知甲种药片每片含5单位的蛋白质和10单位的铁质,售价为3元;乙种药片每片含7单位的蛋白质和4单位的铁质,售价为2元. 若病人每餐至少需要35单位的蛋白质和40单位的铁质,应使甲、乙两种药片各几片才能既满足营养要求又使费用最省?
(19题的答案就在下面,序号出了点问题,敬请原谅!)
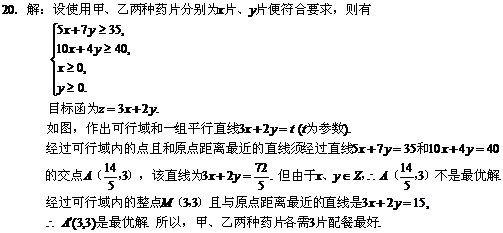
18、(Ⅰ)证明:
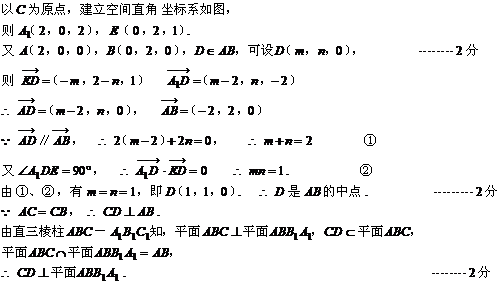
(Ⅱ)解:
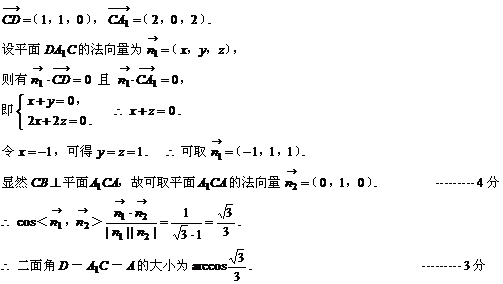
注:用其它方法求解正确者也相应给分。
18、(共13分)
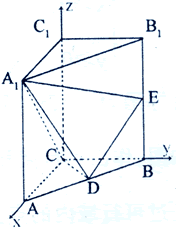
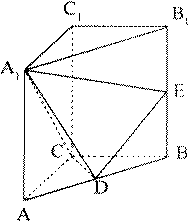
直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E是BB1的中点,
D∈AB,∠A1DE=90°.
(Ⅰ)求证:CD⊥平面ABB1A1;
(Ⅱ)求二面角D-A1C-A的大小.
17.(本小题共14分)
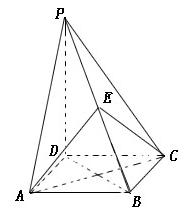 如图,四棱锥
如图,四棱锥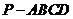 的底面是正方形,
的底面是正方形,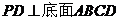 ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面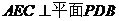 ;
;
(Ⅱ)当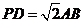 且E为PB的中点时,求AE与
且E为PB的中点时,求AE与
平面PDB所成的角的大小.
[解法1]本题主要考查直线和平面垂直、平面与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力和推理论证能力.
(Ⅰ)∵四边形ABCD是正方形,∴AC⊥BD,
∵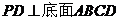 ,
,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面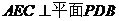 .
.
(Ⅱ)设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∴O,E分别为DB、PB的中点,
∴OE//PD,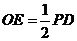 ,又∵
,又∵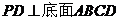 ,
,
∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中,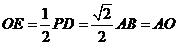 ,
,
∴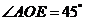 ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为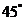 .
.
[解法2]如图,以D为原点建立空间直角坐标系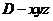 ,
,
设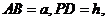
则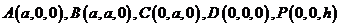 ,
,
(Ⅰ)∵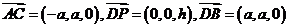 ,
,
∴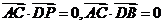 ,
,
∴AC⊥DP,AC⊥DB,∴AC⊥平面PDB,
∴平面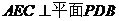 .
.
(Ⅱ)当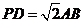 且E为PB的中点时,
且E为PB的中点时,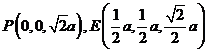 ,
,
设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵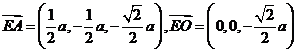 ,
,
∴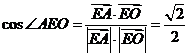 ,
,
∴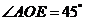 ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为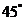 .
.
16.(本小题共12分)已知函数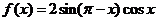 .
.
(Ⅰ)求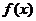 的最小正周期;
的最小正周期;
(Ⅱ)求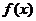 在区间
在区间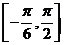 上的最大值和最小值.
上的最大值和最小值.
[解析]本题主要考查特殊角三角函数值、诱导公式、二倍角的正弦、三角函数在闭区间上的最值等基础知识,主要考查基本运算能力.
(Ⅰ)∵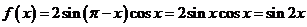 ,
,
∴函数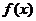 的最小正周期为
的最小正周期为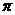 .
.
(Ⅱ)由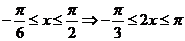 ,∴
,∴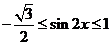 ,
,
∴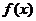 在区间
在区间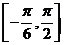 上的最大值为1,最小值为
上的最大值为1,最小值为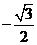 .
.
(一)必做题(11-13题)
11.某篮球队6名主力队员在最近三场比赛中投进的三分球个数如下表所示:
|
队员i |
1 |
2 |
3 |
4 |
5 |
6 |
|
三分球个数 |
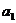 |
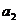 |
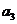 |
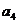 |
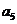 |
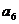 |
图1是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,则图中判断框应填 ,输出的s=
(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
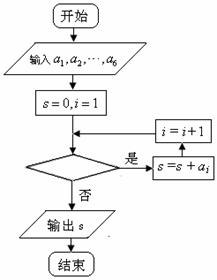


图1
[答案]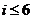 ,
,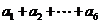
[解析]顺为是统计该6名队员在最近三场比赛中投进的三分球总数的程序框图,所图中判断框应填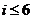 ,输出的s=
,输出的s=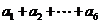 .
.
12.某单位200名职工的年龄分布情况如图2,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是 。若用分层抽样方法,则40岁以下年龄段应抽取 人.
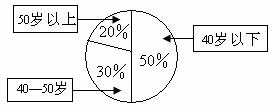
图 2
[答案]37, 20
[解析]由分组可知,抽号的间隔为5,又因为第5组抽出的号码为22,所以第6组抽出的号码为27,第7组抽出的号码为32,第8组抽出的号码为37.
40岁以下年龄段的职工数为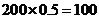 ,则应抽取的人数为
,则应抽取的人数为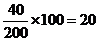 人.
人.
13.以点(2,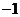 )为圆心且与直线
)为圆心且与直线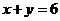 相切的圆的方程是
.
相切的圆的方程是
.
[答案]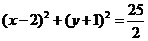
[解析]将直线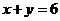 化为
化为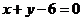 ,圆的半径
,圆的半径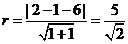 ,所以圆的方程为
,所以圆的方程为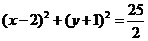


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com