
3、吊汝之孤与汝之乳母:慰问。悬挂。 4、未曾废离:停止;没有用的。
2、至于成立:成年。组织机构等筹备成功,开始存在或(理论、意见)有根据。
1、愿乞终养:希望;愿意、乐。
4、臣密今年四十有四,祖母今年九十有六 又。表示整数和零数之间。
3、零丁孤苦 伶仃,读ling dīng,孤独无靠。
1、内无应门五尺之僮 童;童仆。 2、常在床蓐:褥;草垫子,草席。
2.指数函数的图像和性质是什么?
[互动过程1]
在正整数指数函数中,我们讨论了细胞分裂的个数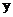 与分裂次数
与分裂次数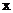 之间的函数关系,这个函数可以表示为指数函数
之间的函数关系,这个函数可以表示为指数函数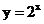 ,而在指数函数中,我们又把正整数指数函数推广到实数指数函数,这样已知分裂的次数我们就可以知道细胞分裂的个数,反过来,如果我们知道分裂细胞的个数,我们同样可以知道细胞分裂的次数,如:求一个这样的细胞经过多少次分裂,大约可以得到1万个细胞,或10万个细胞.这样就可以得到分裂次数
,而在指数函数中,我们又把正整数指数函数推广到实数指数函数,这样已知分裂的次数我们就可以知道细胞分裂的个数,反过来,如果我们知道分裂细胞的个数,我们同样可以知道细胞分裂的次数,如:求一个这样的细胞经过多少次分裂,大约可以得到1万个细胞,或10万个细胞.这样就可以得到分裂次数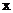 与细胞分裂的个数
与细胞分裂的个数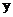 之间的函数关系,那么怎么表示呢?也就是从
之间的函数关系,那么怎么表示呢?也就是从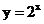 中,用
中,用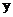 表示出
表示出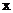 的值.我们学习了对数,就可以把这个函数写成对数的形式就是_______________.
的值.我们学习了对数,就可以把这个函数写成对数的形式就是_______________.
[互动过程2]
思考:对于一般的函数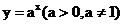 中的两个变量,能不能把
中的两个变量,能不能把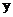 当作自变量,使得
当作自变量,使得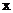 是
是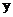 的函数呢?请作出解释.
的函数呢?请作出解释.
思考分析:指数函数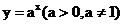 ,对于
,对于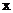 的每一个确定的值,
的每一个确定的值,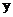 都有唯一的值和它对应;并且当
都有唯一的值和它对应;并且当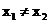 时,___________
,也就是说指数函数反映了数集_______与数集_____________之间的一一对应关系,可见,对于任意的___________,在___中都有唯一的数
时,___________
,也就是说指数函数反映了数集_______与数集_____________之间的一一对应关系,可见,对于任意的___________,在___中都有唯一的数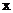 满足
满足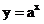 .
.
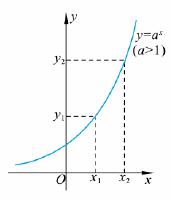
如果把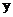 当作自变量,那么
当作自变量,那么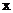 就是
就是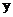 的___________,而且这个函数就是____________,函数_________________叫作对数函数,这里_________________,自变量________.
的___________,而且这个函数就是____________,函数_________________叫作对数函数,这里_________________,自变量________.
[互动过程3]
同学们想一想这种写法与我们原来见过的函数一样吗?怎么不一样?
习惯上,自变量用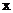 表示,所以这个函数就写成___________________________.
表示,所以这个函数就写成___________________________.
[对数函数的定义]:
我们把函数____________________________叫作对数函数,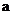 叫作对数函数的底数.
叫作对数函数的底数.
特别地,我们称以10为底的对数函数______________为__________函数;称以无理数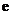 为底的对数函数_____________________为__________________函数.
为底的对数函数_____________________为__________________函数.
例1.计算:(1)计算对数函数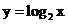 对应于
对应于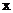 取1,2,4时的函数值;
取1,2,4时的函数值;
(2)计算常用对数函数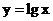 对应于1,10,100,0.1时的函数值.
对应于1,10,100,0.1时的函数值.
[互动过程4]
思考:根据对数函数的定义请同学们思考探讨一下,指数函数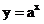 和对数函数
和对数函数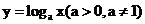 有什么关系?
有什么关系?
[反函数的定义]:
指数函数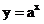 和对数函数
和对数函数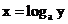 刻画的是同一对变量
刻画的是同一对变量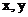 之间的关系,所不同的是:在指数函数
之间的关系,所不同的是:在指数函数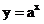 中,
中,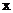 是自变量,
是自变量,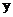 是
是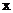 的函数,其定义域是R,值域
的函数,其定义域是R,值域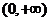 ;在对数函数
;在对数函数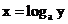 中,
中, 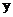 是自变量,
是自变量,
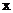 是
是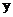 的函数,其定义域是
的函数,其定义域是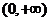 ,值域R.像这样的两个函数叫作____________,就是说,对数函数
,值域R.像这样的两个函数叫作____________,就是说,对数函数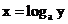 是指数函数
是指数函数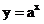
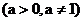 的___________,指数函数
的___________,指数函数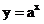 是对数函数
是对数函数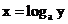 的____________.
的____________.
由于对数函数通常写成_____________________,因此,指数函数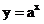
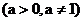 是对数函数______________________的反函数;同时,对数函数_______________________也是指数函数
是对数函数______________________的反函数;同时,对数函数_______________________也是指数函数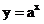
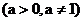 的反函数.
的反函数.
例2.写出下列对数函数的反函数: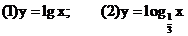
例3.写出下列指数函数的反函数:
(1)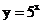 ; (2)
; (2)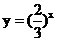
练习.1,2,3,4
作业:习题3-5.A组1,2
3、情感.态度与价值观
通过学习对数函数,了解指数函数与对数函数之间的关系.在学习的过程中体会研究函数要紧扣函数的定义去理解对应关系.增强学习对数函数的积极性和自信心.
[学习重点]: 对数函数的定义的理解以及对数函数与指数函数的关系.
[学习难点]:对数函数与支书函数之间的关系.
[学习方法]:思考、探究、领悟.
[学习过程]
[新课导入]
[互动过程1]
复习:1.对数是怎么定义的?对数与指数之间的关系是什么?什么是函数?什么是指数函数?
2、 过程与方法 
(1)掌握指数函数与对数函数之间的关系.
(2)学会问题的转化,常规思维的迁移.
1、知识与技能
(1) 由前面学习指数函数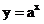 的基础上,根据函数的定义引入对数函数.
的基础上,根据函数的定义引入对数函数.
(2)
能够理解指数函数与对数函数的关系,理解反函数的定义.
(3) 会求指数函数与对数函数的反函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com