
10.在区间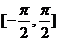 上随机取一个数x,
上随机取一个数x,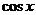 的值介于0到
的值介于0到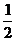 之间的概率为(
).
之间的概率为(
).
A.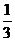 B.
B. C.
C.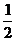 D.
D.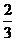


[解析]:在区间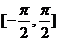 上随机取一个数x,即
上随机取一个数x,即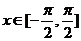 时,要使
时,要使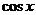 的值介于0到
的值介于0到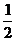 之间,需使
之间,需使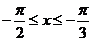 或
或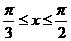 ,区间长度为
,区间长度为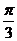 ,由几何概型知
,由几何概型知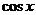 的值介于0到
的值介于0到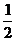 之间的概率为
之间的概率为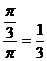 .故选A.
.故选A. 

答案:A
[命题立意]:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值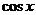 的范围,再由长度型几何概型求得.
的范围,再由长度型几何概型求得.
9. 设斜率为2的直线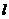 过抛物线
过抛物线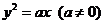 的焦点F,且和
的焦点F,且和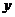 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).


A.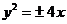 B.
B.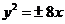 C.
C. 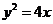 D.
D. 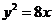
[解析]: 抛物线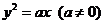 的焦点F坐标为
的焦点F坐标为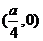 ,则直线
,则直线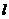 的方程为
的方程为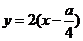 ,它与
,它与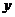 轴的交点为A
轴的交点为A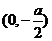 ,所以△OAF的面积为
,所以△OAF的面积为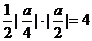 ,解得
,解得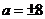 .所以抛物线方程为
.所以抛物线方程为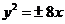 ,故选B.
,故选B. 

答案:B.
[命题立意]:本题考查了抛物线的标准方程和焦点坐标以及直线的点斜式方程和三角形面积的计算.考查数形结合的数学思想,其中还隐含着分类讨论的思想,因参数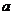 的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
8. 已知α,β表示两个不同的平面,m为平面α内的一条直线,则“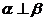 ”是“
”是“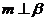 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件
D.既不充分也不必要条件 

[解析]:由平面与平面垂直的判定定理知如果m为平面α内的一条直线,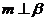 ,则
,则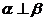 ,反过来则不一定.所以“
,反过来则不一定.所以“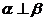 ”是“
”是“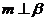 ”的必要不充分条件
”的必要不充分条件 
 .
.
答案:B.
[命题立意]:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
7.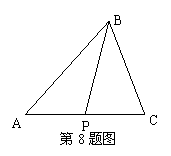 设P是△ABC所在平面内的一点,
设P是△ABC所在平面内的一点,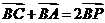 ,则( )
,则( )
A.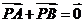 B.
B. 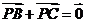 C.
C. 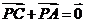 D.
D.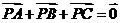
[解析]:因为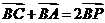 ,所以点P为线段AC的中点,所以应该选B。
,所以点P为线段AC的中点,所以应该选B。
答案:B.
[命题立意]:本题考查了向量的加法运算和平行四边形法则, 

可以借助图形解答。
6. 定义在R上的函数f(x)满足f(x)= 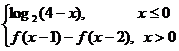 ,则f(3)的值为( )
,则f(3)的值为( )
A.-1 B. -2 C.1 D. 2
[解析]:由已知得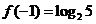 ,
,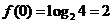 ,
,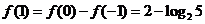 ,
,
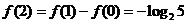 ,
,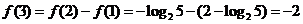 ,故选B.
,故选B.
答案:B. 

[命题立意]:本题考查对数函数的运算以及推理过程..
5.D [命题意图]此题主要考查了平面向量的坐标运算,通过平面向量的平行和垂直关系的考查,很好地体现了平面向量的坐标运算在解决具体问题中的应用[解析]不妨设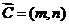 ,则
,则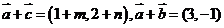 ,对于
,对于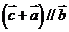 ,则有
,则有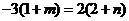 ;又
;又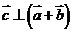 ,则有
,则有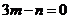 ,则有
,则有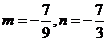
5.已知向量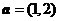 ,
,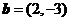 .若向量
.若向量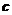 满足
满足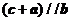 ,
,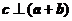 ,则
,则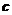
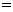 (
)
(
)
A.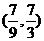 B.
B.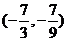 C.
C.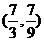 D.
D.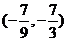
4.C [命题意图]此题主要考查立体几何的线面、面面的位置关系,通过对平行和垂直的考查,充分调动了立体几何中的基本元素关系.
[解析]对于A、B、D均可能出现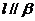 ,而对于C是正确的.
,而对于C是正确的. 

4.设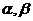 是两个不同的平面,
是两个不同的平面,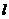 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若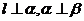 ,则
,则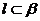 B.若
B.若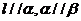 ,则
,则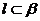
C.若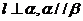 ,则
,则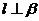 D.若
D.若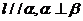 ,则
,则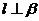
3.D [命题意图]本小题主要考查了复数的运算和复数的概念,以复数的运算为载体,直接考查了对于复数概念和性质的理解程度.
[解析]对于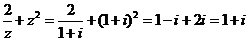


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com