
1.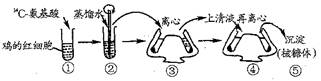 在下列实验装置①号试管中加入14C氨基酸一段时间后,按图示方法步骤进行处理。其相关叙述中,错误的是
在下列实验装置①号试管中加入14C氨基酸一段时间后,按图示方法步骤进行处理。其相关叙述中,错误的是
A.鸡的红细胞在蒸馏水中也会发生渗透作用吸水,最终可导致细胞破裂
B.14C氨基酸进入鸡的红细胞内的方式与小麦根尖表皮细胞吸收K+的方式相同
|
D.除去细菌或蓝藻的细胞壁后按上图同样的方法步骤处理,结果得不到核糖体
22.解:(1)∵ 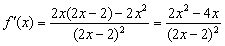 ,
,
∴ 由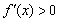 有x<0或x>2,由
有x<0或x>2,由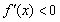 有0<x<2且x≠1,
有0<x<2且x≠1,
即f (x)的单调递增区间为(-∞,0),(2,+∞),单调递减区间为(0,1),(1,2).
………………………………………………………………………………………4分
(2)由题有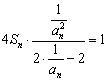 ,整理得2Sn=an(1-an), ①
,整理得2Sn=an(1-an), ①
∴ 当n=1时,2S1=a1(1-a1),解得a1=-1,或a1=0(舍).
当n≥2时,2Sn-1=an-1(1-an-1), ②
于是①-②得2an=an-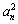 -an-1+
-an-1+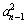 ,
,
整理得an+an-1=(an-1-an)(an-1+an),
由已知有an+an-1≠0,
∴ an-an-1=-1(常数).
∴ {an}是以-1为首项,-1为公差的等差数列.
∴ an=-n.………………………………………………………………………9分
(3)∵ an=-n,
∴ 原不等式即为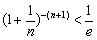 ,等价于
,等价于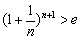 .
.
两边同取对数得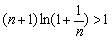 ,
,
即证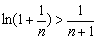 .
.
构造函数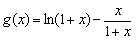 ,
,
∵ 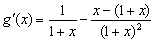
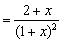 ,
,
显然当x≥0时,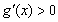 ,
,
∴ g(x)在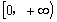 上是增函数.
上是增函数.
∴ 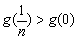 ,即
,即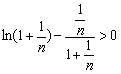 ,整理即得
,整理即得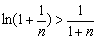 .
.
故原不等式得证.………………………………………………………………14分
21.解:(1)设-e≤x<0,则0<-x≤e,
∴ f (-x)=a(-x)+ln(-x),
已知f (x)是奇函数可得f (-x)=-f (x).
∴ -f (x)=-ax+ln(-x),即f (x)=ax-ln(-x).
∴ f (x)=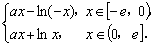 ………………………………………………4分
………………………………………………4分
(2)x∈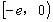 时,
时,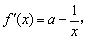
令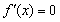 ,得
,得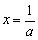 .…………………………………………………………5分
.…………………………………………………………5分
①当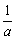 ≤-e,即-
≤-e,即-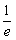 ≤a<0时,
≤a<0时,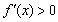 .
.
故f (x)在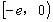 上是增函数.
上是增函数.
∴ f (x)min=f (-e)=-ae-1=3,
解得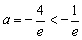 (舍).………………………………………………………8分
(舍).………………………………………………………8分
②当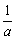 >-e,即
>-e,即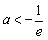 时,则
时,则
|
x |
[-e,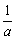 ) ) |
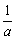 |
(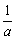 ,0) ,0) |
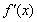 |
- |
0 |
+ |
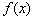 |
↘ |
最小值 |
↗ |
∴ f (x)min=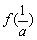 =
=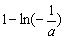 =3,解得
=3,解得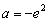 .
.
综上所述,存在实数a=-e2满足条件.………………………………………12分
20.解:(1)令y=f (x)=ax+2-1,于是y+1=ax+2,
∴ x+2=loga(y+1),即x=loga(y+1)-2,
∴ 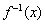 =loga(x+1)-2(x>-1).………………………………………………3分
=loga(x+1)-2(x>-1).………………………………………………3分
(2)当0<a<1时,
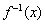 max=loga(0+1)-2=-2,
max=loga(0+1)-2=-2,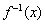 min=loga(1+1)-2=loga2-2,
min=loga(1+1)-2=loga2-2,
∴ -2-(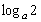 -2)=2,解得
-2)=2,解得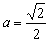 或
或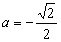 (舍).
(舍).
当a>1时,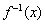 max=loga2-2,
max=loga2-2,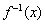 min=-2,
min=-2,
∴ 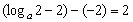 ,解得
,解得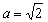 或
或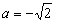 (舍).
(舍).
∴ 综上所述,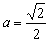 或
或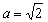 .……………………………………………7分
.……………………………………………7分
(3)由已知有loga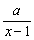 ≤loga(x+1)-2,
≤loga(x+1)-2,
即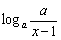 ≤
≤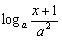 对任意的
对任意的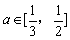 恒成立.
恒成立.
∵ 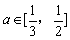 ,
,
∴ 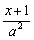 ≤
≤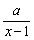 .①
.①
由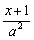 >0且
>0且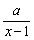 >0知x+1>0且x-1>0,即x>1,
>0知x+1>0且x-1>0,即x>1,
于是①式可变形为x2-1≤a3,
即等价于不等式x2≤a3+1对任意的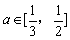 恒成立.
恒成立.
∵ u=a3+1在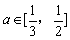 上是增函数,
上是增函数,
∴ 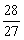 ≤a3+1≤
≤a3+1≤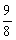 ,于是x2≤
,于是x2≤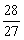 ,
,
解得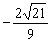 ≤x≤
≤x≤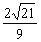 .
.
结合x>1得1<x≤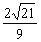 .
.
∴ 满足条件的x的取值范围为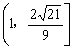 .…………………………………12分
.…………………………………12分
19.解:(1)设{an}的公差为d,{bn}的公比为q,则由题意可列方程组
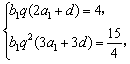 ……………………………………………………………3分
……………………………………………………………3分
把a1=3,b1=1代入解得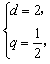 或
或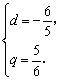
∵ {an}的各项均为正,
∴ 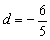 应舍去.
应舍去.
∴ 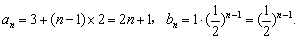 ……………………………5分
……………………………5分
(2)∵ 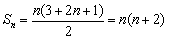 ,
,
∴ Tn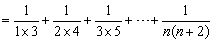
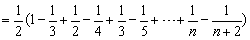
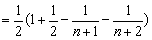 ,
,
=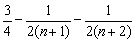 . …………………………………………………9分
. …………………………………………………9分
∴ 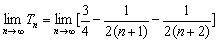 =
=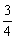 ,即
,即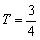 ,
,
∴ 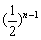 ≥
≥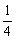 ,
,
解得 n≤3,
∴ 正整数n=1,2,3. ………………………………………………………12分
18.解:(1)设有x人患“甲流感”,则由题意有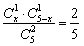 , ……………3分
, ……………3分
解得 x=1或x=4(舍).
∴ 这5位发热病人中有1人患“甲流感”.…………………………………5分
(2)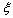 =1,2,3,4,则
=1,2,3,4,则
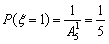 ,
,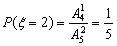 ,
,
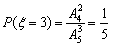 ,
,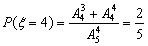 .
.
∴ 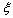 的分布列为
的分布列为
|
ξ |
1 |
2 |
3 |
4 |
|
P |
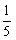 |
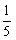 |
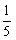 |
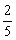 |
……………………………………………………………………………………10分
∴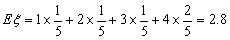 .
……………………………………12分
.
……………………………………12分
17.解:由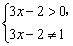 解得
解得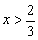 且x≠1,即A={x|
且x≠1,即A={x|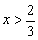 且x≠1},
且x≠1},
由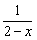 ≥1解得1≤x<2,即B={x|1≤x<2}.
………………………………4分
≥1解得1≤x<2,即B={x|1≤x<2}.
………………………………4分
(1)于是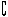 RA={x|x≤
RA={x|x≤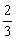 或x=1},所以(
或x=1},所以(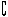 RA)∩B={1}. ……………………7分
RA)∩B={1}. ……………………7分
(2)∵ A∪B={x|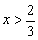 },即C={x|
},即C={x|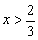 }.
}.
由|x-a|<4得a-4<x<a+4,即M={x|a-4<x<a+4}.
∵ M∩C=Æ,
∴ a+4≤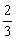 ,解得a≤
,解得a≤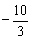 .…………………………………………………12分
.…………………………………………………12分
13.0 14.500 15.-π 16.②⑤
BCCAD DABAC DB
22.(本题满分14分)已知函数f (x)=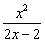 (x≠1),各项同号且均不为零的数列{an}的前n项和Sn满足4Sn·f (
(x≠1),各项同号且均不为零的数列{an}的前n项和Sn满足4Sn·f (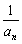 )=1(n∈N*).
)=1(n∈N*).
(1)试求f (x)的单调递增区间和单调递减区间;
(2)求数列{an}的通项公式;
(3)求证: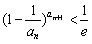 .(e为自然对数的底数)
.(e为自然对数的底数)
绵阳市高中2010届高三第一次诊断性考试
数学(理)参考解答及评分标准
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com