
18.(本小题满分12分)
[解]方法一:(Ⅰ)取BC的中点N,连结MN.
由已知,PM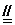 CN,则MN
CN,则MN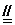 PC,所以MN⊥平面ABC.
(1分)
PC,所以MN⊥平面ABC.
(1分)
过点N作NH⊥AC,交AC的延长线于H,连结MH,
由三垂线定理知,AC⊥MH.
所以∠MHN为二面角M-AC-B的平面角. (3分)
连结AN,在△ACN中,由余弦定理,得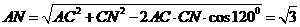 .
.
 由已知∠AMN=60°,在Rt△ANM中,
由已知∠AMN=60°,在Rt△ANM中,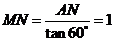 .
(6分)
.
(6分)
在Rt△CHN中,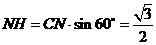 .
(7分)
.
(7分)
在Rt△MNH中,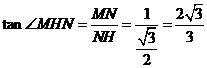 .
.
故二面角M-AC-B的正切值是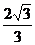 .
(8分)
.
(8分)
(Ⅱ)因为四边形PCNM为正方形,MN⊥平面ABC,则
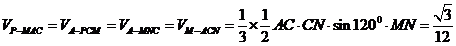 .
(12分)
.
(12分)
 方法二:(Ⅰ)在平面ABC内,过点C作CB的垂线,
方法二:(Ⅰ)在平面ABC内,过点C作CB的垂线,
按如图所示建立空间直角坐标系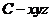 .
(1分)
.
(1分)
设点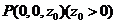 ,由已知可得,点
,由已知可得,点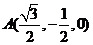 ,
,
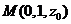 ,则
,则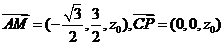 .
.
因为直线AM与直线PC所成的角为60°,则
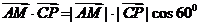 ,即
,即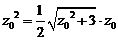 .
.
解得z0=1,从而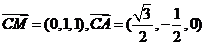 .
(3分)
.
(3分)
设平面MAC的一个法向量为n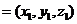 ,则
,则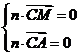 ,即
,即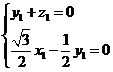 .
.
取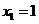 ,则n
,则n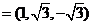 .
(5分)
.
(5分)
又m=(0,0,1)为平面ABC的一个法向量,设向量m与n的夹角为θ,则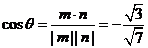 .
.
从而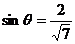 ,
,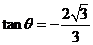 .
(7分)
.
(7分)
显然,二面角M-AC-B的平面角为锐角,故二面角M-AC-B的正切值是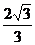 . (8分)
. (8分)
(Ⅱ)因为a=(1,0,0)为平面PCM的一个法向量,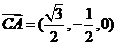 ,则
,则
点A到平面PCM的距离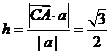 .
(10分)
.
(10分)
又PC=PM=1,则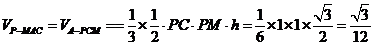 . (12分)
. (12分)
17.(本小题满分12分)
[解](Ⅰ)记抽取的5张门票中“恰有3个景点”为事件A,“恰有4个景点”为事件B.
若抽取的5张门票中恰有3个景点,则至少要抽取2张张家界门票,
所以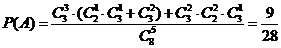 .
(2分)
.
(2分)
若抽取的5张门票中恰有4个景点,则至多只能抽取2张张家界门票,
所以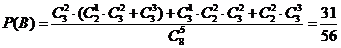 .
(5分)
.
(5分)
因为事件A,B互斥,所以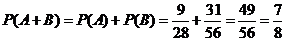 .
.
故抽取的5张门票中恰有3个或恰有4个景点的概率是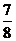 .
(6分)
.
(6分)
(Ⅱ)因为5张门票中至少含有2个景点,则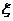 的可能取值为10,8,6,4.
(7分)
的可能取值为10,8,6,4.
(7分)
其中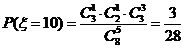 ,
,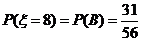 ,
,
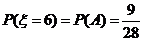 ,
,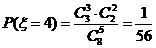 .
(10分)
.
(10分)
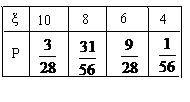 所以
所以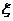 的分布列为
.
(11分)
的分布列为
.
(11分)
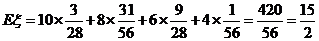
16、(本小题满分12分)
f(x)=cos(2x+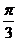 )+sin
)+sin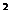 x.=
x.=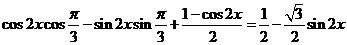
所以函数f(x)的最大值为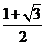 ,最小正周期
,最小正周期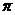 .
. 

(2)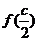 =
=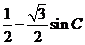 =-
=-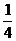 , 所以
, 所以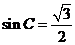 ,
,
因为C为锐角, 所以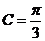 ,
,
又因为在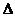 ABC 中, cosB=
ABC 中, cosB=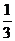 , 所以
, 所以 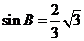 , 所以
, 所以


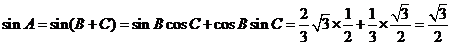 .
.
13. : 14. :
15
11. 6 12. 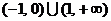
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
第II卷(非选择题 共100分)
21.(本小题满分13分)
给出定义在(0,+∞)上的三个函数: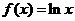 ,
,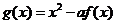 ,
,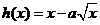 ,已知
,已知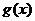 在x=1处取极值.
在x=1处取极值.
(Ⅰ)确定函数h(x)的单调性;
(Ⅱ)求证:当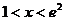 时,恒有
时,恒有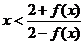 成立;
成立;
(Ⅲ)把函数h(x)的图象向上平移6个单位得到函数h1(x)的图象,试确定函数y=g(x)-h1(x)的零点个数,并说明理由.

 安徽省灵璧中学高三第三次月考数学试卷答题卷
安徽省灵璧中学高三第三次月考数学试卷答题卷
( 文 科 )
满分150分,考试时间120分钟
19.(本小题满分13分)
设椭圆E: 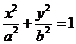 (a,b>0)过M(2,
(a,b>0)过M(2,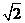 ) ,N(
) ,N( ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(I)求椭圆E的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且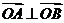 ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
18.(本小题满分12分)
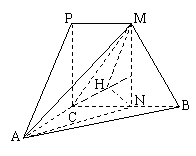
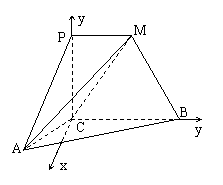
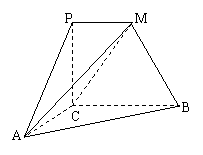 如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
(Ⅰ)求二面角M-AC-B大小的正切值;
(Ⅱ)求三棱锥P-MAC的体积.
17. 湖南省有许多旅游景点,某同学利用寒暑假旅游了张家界、南岳、韶山、岳阳楼和桃花源等5个景点,并收藏有张家界纪念门票3张,南岳纪念门票2张,韶山、岳阳楼、桃花源纪念门票各1张,现从中随机抽取5张.
(Ⅰ)求抽取的5张门票中恰有3个或恰有4个景点的概率;
(Ⅱ)若抽取的5张门票中5个景点都有记10分,恰有4个景点记8分,恰有3个景点记6分,依此类推.设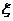 表示所得的分数,求
表示所得的分数,求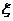 的分布列和数学期望.
的分布列和数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com