2、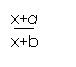　　　 >0型不等式转化结果:(x+a)(x+b)>0

1、(x+a)(x+b)<0型不等式转化方法是 　　　　与

2.分式不等式　　 >0的解法

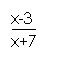
比较　　 〈0与(x-3)(x+7)<0与的解集

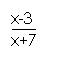思考：　 　〈0与(x-3)(x+7)<0的解集，是否相同.

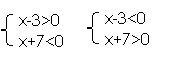
它们都可化为一次不等式组　 　　　与

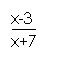
[例5]　 解不等式　　　 <0

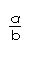
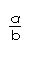
解析：这个不等式若要正确无误地求出解集，则必须实现转化，而这个转化依据就是　　 >0　　　 ab>0及 　　<0　　 　ab<0

解：这个不等式解集是不等式组

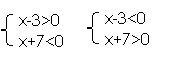
　　　　 与　　　　　 的解集的并集.

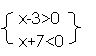
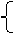
　　　　 由 x　　　　　 ={x|-7<x<3}

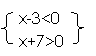
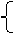
　x|　　　　　 =f

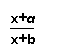得原不等式的解集是{x|-7<x<3}∪f　 ={x|-7<x<3}

由些得出不等式　　 >0的解法同(x+a)(x+b)>0的解法相同.

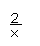
[例]　 求不等式3+　 <0的解集.

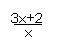
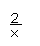
解：3+　 <0可变形为　　 <0.

　 转化为(3x+2)x<0

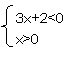
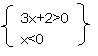
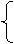
　 x|　　　　　　 ∪　 x|

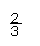
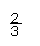={x|-　 <x<0 }∪f ={x|-　 <x<0 }

Ⅲ 课堂练习：

2、x(x-2)>8

解：将x(x-2)>8变形为x²-2x-8>0化成积的形式为(x-4)(x+2)>0

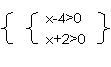
x|　　　　　　　 ={x|x>4}

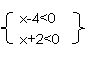
x|　　　　　　　 ={x|x<-2}

原不等式的解集为{x|x>4}∪{x|x<-2} ={x|x<-2或x>4}

说明：问题解决的关键在于通过正确因式分解,将不等号左端化成两个一次因式积的形式.

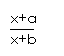
1、　　　　　　　 x²-3x-4>0

解：将x²-3x-4>0分解为(x-4)(x+1)>0

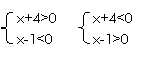
转化为　　　 与

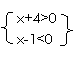
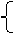
由 x|x　　　　　 ={x|-4<x<1}

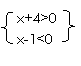
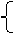
由 x|x　　　　　 =f

原不等式的解集为{x|x>4}∪{x|x<-1}={x|x<-1或x>4}

1.一元二次不等式(x+a)(x+b)<0的解法:

首先我们来观察这个不等式(x+4)(x-1)<0的特点，以不等式两边来观察.

特点：左边是两个x一次因式的积，右边是0.

思考：依据该特点，不等式能否实现转化而又能转化成什么形式的不等式？

不等式(x+4)(x-1)<0可以实现转化，可转化成一次不等式组：

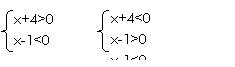
　　 与

注意：不等式(x+4)(x-1)<0的解集是上面不等式组解集的并集.

一元二次不等式(x+4)(x-1)<0的解法：

解：将(x+4)(x-1)<0转化为

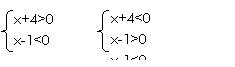
　　　　 与

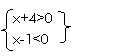
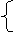
由 x|　　　　 ={x|-4<x<-1}

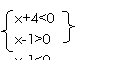
　　　　　　 =f

得原不等式的解集是{x|-4<x<1}∪f　 ={x|-4<x<1}

步骤：从上可看出一般形式(x+a)(x+b)<0解的步骤：

将所解不等式转化为一次不等式组,求其解集的并集，即为所求不等式的解.

通过因式分解，转化为一元一次不等式组的方法,

[例]　 求解下列不等式.

3、　　　　　　　 数形结合思想运用.

Ⅱ 新课讲授

2、　　　　　　　 一元二次不等式的解法.

通过问题求解过程，渗透..

　教学重点　　　　　　　　

一元二次不等式求解.

　教学难点　　　　　　　　

将已知不等式等价转化成合理变形式子.

教学方法　　　　　　　　

创造教学法

为使问题得到解决，关键在于合理地将已知不等式变形，变形的过程也是一个创造的过程，只有这一过程完成好，本节课的难点也就突破.

　教学过程　　　　　　　　

Ⅰ 课题导入

1、　　　　　　　 一元二次方程、二次函数、一元二次不等式的关系.

2、　　　　　　　 通过问题求解渗透分类讨论思想，提高逻辑思维能力.